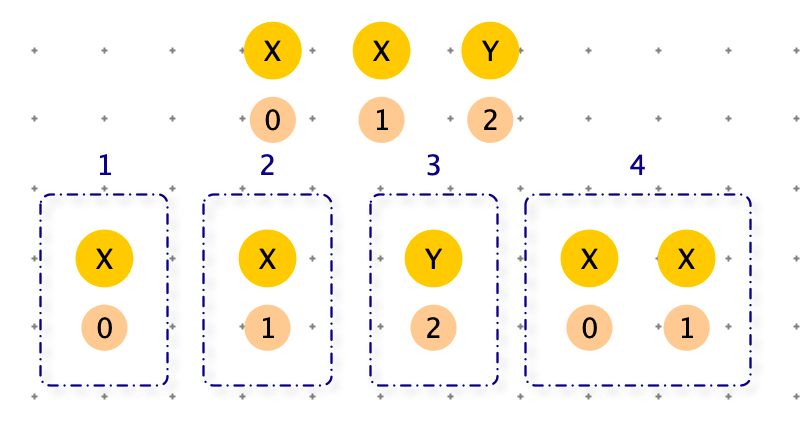
给定一个字符串 str,能否从字符串中移除部分(0个或多个)字符使其变为回文串,此处空串认为是回文串,求多少移除方案。(注意:相同字符的由于的移除,认为不同的移除方案)。
【例如】str = “XXY” 有 4 中移除方案
方案一:暴力规划
移除字符与保留字符效果是一样的。
可能性尝试:范围尝试模型。
f( i , j ) 定义:str[ i: j+1 ] 子串中包含回文个数。最终结果:f ( 0, len(str) - 1 )
可能性分类:
| 开头 | 结尾 | |
|---|---|---|
| ① | 以 i 开头 | 以 j 结尾 |
| ② | 不以 i 开头 | 以 j 结尾 |
| ③ | 不以 i 开头 | 不以 j 结尾 |
| ④ | 以 i 开头 | 不以 j 结尾 |
以上所有分类:互斥。最终的解是所有可能性的全集:求和。
要求 f (i,j) 解,必须先得到 f( i, j) 最近的子问题
f ( i, j-1 ) 是 str[ i: j ]子串中包含回文个数,不包含字符 str[j] ,所以以 j 结尾的可能性都不可能。
f ( i, j-1 ) = ③ + ④
同理:
f ( i+1, j ) = ② + ③
f ( i+1, j-1 ) = ③
现在缺少可能性 ①
可能性① 要求:以 i 开头且以 j 结尾。如果str[i] != str[j],不可能出现可能性 ①
此时结果:f ( i, j ) = f ( i, j-1 ) + f ( i+1, j ) - f ( i+1, j-1 ) = (③ + ④)+ ( ② + ③)- ③ = ② + ③ + ④
如果str[i] == str[j]:不可能出现可能性 ③,③ = 0
f ( i, j ) = f ( i, j-1 ) + f ( i+1, j ) + 1 = ② + ④ + 1
1 是 str[i]str[j] 这个回文串
def min_remove(string):
if not string: return 0
return f(string, 0, len(string) - 1)
def f(string, i, j):
if i == j: return 1
if i + 1 == j: return 3 if string[i] == string[j] else 2
res = f(string, i, j - 1) + f(string, i + 1, j)
if string[i] == string[j]:
res += 1
else:
res -= f(string, i + 1, j - 1)
return res
方案二:动态规划
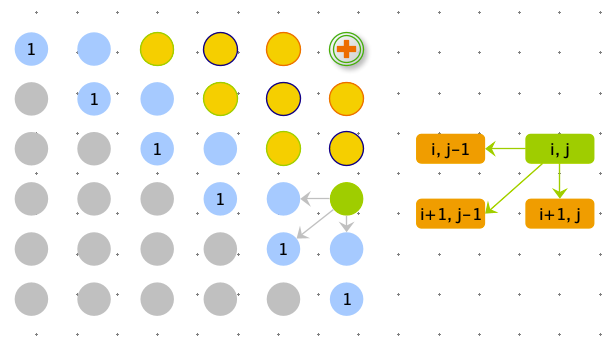
def min_remove2(string):
if not string: return 0
n = len(string)
dp = [[0] * n for _ in range(n)]
dp[-1][-1] = 1
for i in range(n - 1):
dp[i][i] = 1
dp[i][i + 1] = 3 if string[i] == string[i + 1] else 2
for row in range(n - 3, -1, -1):
for col in range(row + 2, n):
dp[row][col] = dp[row][col - 1] + dp[row + 1][col]
if string[row] == string[col]:
dp[row][col] += 1
else:
dp[row][col] -= dp[row + 1][col - 1]
return dp[0][-1]
方案三:动态规划–滚动数组
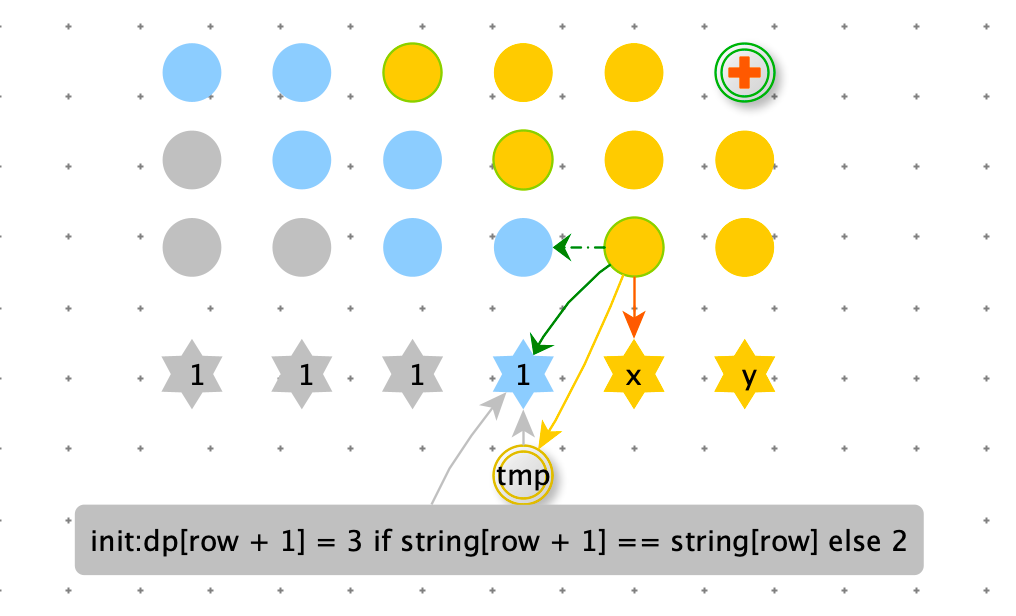
def min_remove3(string):
if not string: return 0
if len(string) == 1: return 1
n = len(string)
dp = [1] * n
dp[-1] = 3 if string[-1] == string[-2] else 2
for row in range(n - 3, -1, -1):
tmp = 1
dp[row + 1] = 3 if string[row + 1] == string[row] else 2
for col in range(row + 2, n):
new_value = dp[col - 1] + dp[col]
if string[row] == string[col]:
new_value += 1
else:
new_value -= tmp
tmp = dp[col]
dp[col] = new_value
return dp[-1]
对数器
import random
def generator_random_str(max_size):
alphabet = [chr(i) for i in range(97, 105)]
size = int(random.random() * max_size)
return ''.join([random.sample(alphabet, 1)[0] for _ in range(size)])
def check():
max_size = 10
for i in range(500):
stirng1 = generator_random_str(max_size)
res1 = min_remove(stirng1)
res2 = min_remove2(stirng1)
res3 = min_remove3(stirng1)
if res1 != res2 or res1 != res3:
print("ERROR", stirng1, "res1=", res1, "res2=", res2, "res3=", res3)
print("OVER")
check()
总结:本题考察是范围尝试模型,难点在于可能性分类后,要组合出最终的答案。