给定一个字符串 str,返回把 str 全部切成回文子串的最小切割数。
【举例】
str = “ABA” 不需要切割,str 本身就是回文串,所以返回 0
str = “ACDCDCDAD” 最少需要切 2 次变成 3 个回文子串,比如“A”、“CDCDC” 和 “DAD”,所以返回 2.
方案一:暴力递归
动态规划:从左向右尝试模型。不是字符每个位置都可以作为切分点。左边部分必须是一个回文子串,才有资格作为切分点。
f( i ) 定义: str[ i: ] 子串中回文子串的个数。
最终结果:f(0) - 1。整个字符串中回文子串的个数 = 最小切割数 + 1
可能性分析:
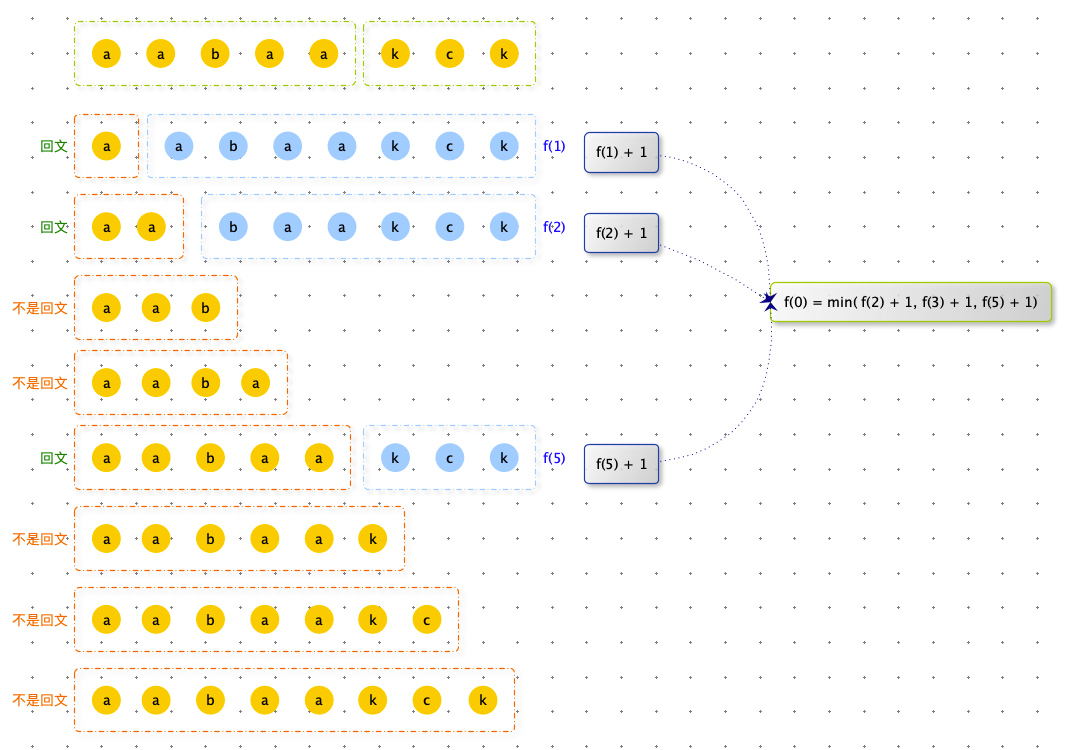
如下图:str[ :j ] 是回文(个数是1),此时 j 就是一个切分点,f ( j ) 是后半部分包含的回文子串的个数,因此整体个数时:f ( j ) + 1。题意要求最小切割数,所以最终结果是:所有切分点的最小值。
import sys
def min_cut(string):
return f(string, 0) - 1
def f(string, index):
if index == len(string): return 0
res = sys.maxsize
for i in range(index, len(string)):
if valid(string, index, i):
res = min(res, f(string, i + 1) + 1)
return res
def valid(string, i, j):
while i <= j:
if string[i] != string[j]:
return False
i += 1
j -= 1
return True
# a|cdcdc|ada
print(min_cut("acdcdcada"))
# aabaa|kck
print(min_cut("aabaakck"))
方案二:动态规划
时间复杂度:$O(N^3)$
空间复杂度:$O(N)$
def min_cut2(string):
if not string: return 0
dp = [0] * (len(string) + 1)
for i in range(len(string) - 1, -1, -1):
res = sys.maxsize
for j in range(i, len(string)):
if valid(string, i, j):
res = min(res, dp[j + 1] + 1)
dp[i] = res
return dp[0] - 1
def valid(string, i, j):
while i <= j:
if string[i] != string[j]:
return False
i += 1
j -= 1
return True
方案三:动态规划–优化判断是否是回文串
在判断 str 每个子串是不是回文时,都需要 O(N) 的时间复杂度。其实我们可以提前计算好,在使用时直接查询结果。
生成回文串矩阵,dp[i][j] 为 True 表示以 i 开头,以 j 结尾的 str 是回文串,dp[i][j] 为 False 表示不是回文串。
dp 的生成使用了在动态规划的范围探索模型。
可能性分析:
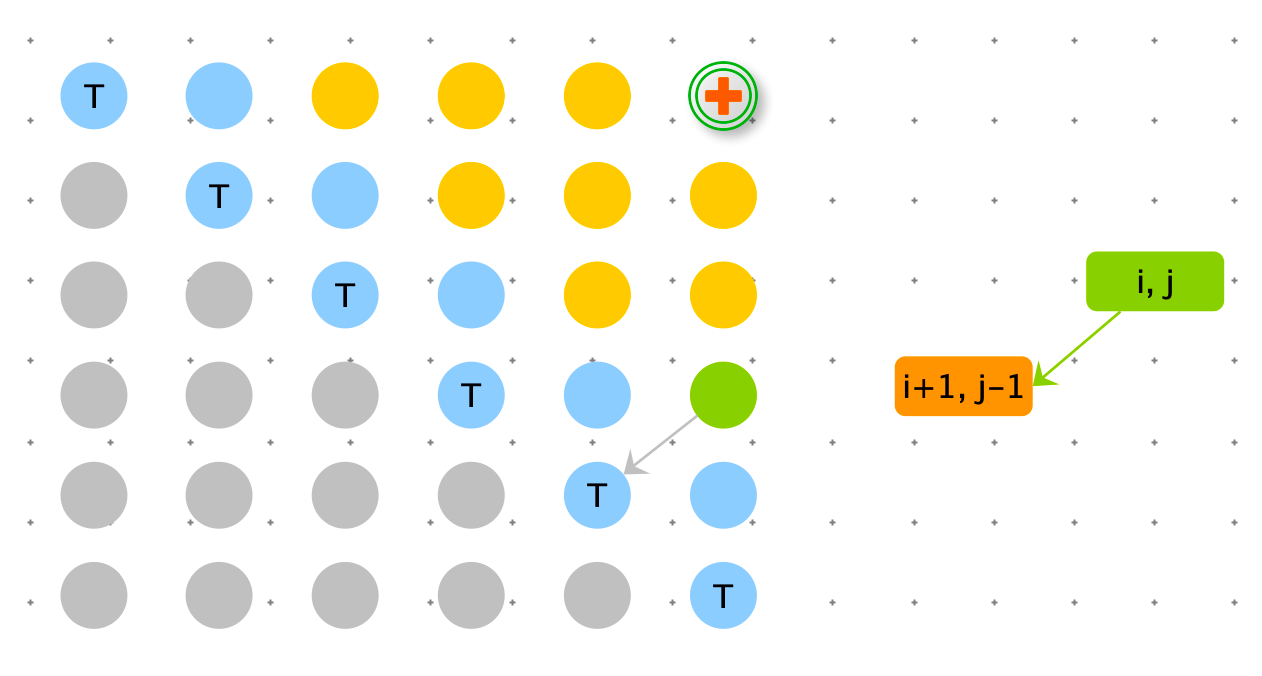
$f(i,j)=\begin{cases} dp[i+1][j-1] &str[i]==str[j] \False &str[i]!=str[j] \end{cases}$
- 如果 str[i] == str[j],str[ i: j+1 ] 是否是回文串取决于去掉 i 和 j 后的子串是不是回文串。
- str[i] != str[j],str[ i: j+1 ] 一定不是回文串
basecase:
- 只有一个字符时,一定为回文串:dp[i][i] = True
- 只有两个个字符时,这两个字符相等为回文串,不相等就不是回文串。
时间复杂度:$O(N^2)$
空间复杂度:$O(N^2)$
def palindrome(string):
n = len(string)
dp = [[False] * n for _ in range(n)]
# base case
dp[-1][-1] = True
for i in range(n - 1):
dp[i][i] = True
dp[i][i + 1] = string[i] == string[i + 1]
for row in range(n - 3, -1, -1):
for col in range(row + 2, n):
dp[row][col] = string[row] == string[col] and dp[row + 1][col - 1]
return dp
将 valid 调用改为从提前计算好的 palindrome_dp 中查询。
时间复杂度:$O(N^2)$
空间复杂度:$O(N^2)$
def min_cut3(string):
if not string: return 0
dp = [0] * (len(string) + 1)
palindrome_dp = palindrome(string)
for i in range(len(string) - 1, -1, -1):
res = sys.maxsize
for j in range(i, len(string)):
if palindrome_dp[i][j]:
res = min(res, dp[j + 1] + 1)
dp[i] = res
return dp[0] - 1
对数器
import random
def generator_random_str(max_size):
alphabet = [chr(i) for i in range(97, 123)]
size = int(random.random() * max_size)
return ''.join([random.sample(alphabet, 1)[0] for _ in range(size)])
def check():
max_size = 10
for i in range(500):
stirng1 = generator_random_str(max_size)
res1 = min_cut(stirng1)
res2 = min_cut2(stirng1)
res3 = min_cut3(stirng1)
if res1 != res2 or res2 != res3:
print("ERROR", stirng1, "res1=", res1, "res2=", res2, "res3=", res3)
print("OVER")
check()
总结:本题在求回文子串的最小切割数时,使用动态规划从左向右尝试模型。但是在判断子串是不是回文串时,又使用了动态规划的范围尝试模型。本题综合使用了两种尝试模型。
