给定一个字符串 str,求最长的回文子序列。
动态规划:范围尝试模型
**范围尝试模型一般根据开头和结尾讨论可能性**f( i , j) 在 str [i:j+1] 上最长回文子序列的长度,终止要求的是 f (0 , len(str)-1)
可能性分析:
$f(i,j)=\begin{cases} f(i-1,j-1)+2 & ;str[i]==str[j] \ max(f(i-1,j),f(i,j-1)) &;str[i]!=str[j] \end{cases}$
- 如果 str[i]==str[j] ,则是在原有 f(i-1,j-1) 子问题的基础上加 2
- 如果 str[i] != str[j] ,则回退到最近的子问题,求最大值
basecase
- 当 i == j 时,如果 str[i] == str[j] 返回 1,否则返回 0。
- 当 i == j + 1 时,如果 str[i] == str[j] 返回 2,否则返回 0。
方案一:暴力递归
def max_sub_palindrome(string):
if not string: return 0
t = f(string, 0, len(string) - 1)
return t
def f(string, i, j):
if i == j:
return 1
if i == j + 1 or i + 1 == j:
return 2 if string[i] == string[j] else 1
if string[i] == string[j]:
return f(string, i + 1, j - 1) + 2
return max(f(string, i + 1, j), f(string, i, j - 1))
方案二:动态规划

def max_sub_palindrome2(string):
if not string: return 0
n = len(string)
dp = [[0] * n for _ in range(n)]
# base case
for i in range(n):
dp[i][i] = 1
for i in range(n - 2, -1, -1):
for j in range(i + 1, n):
if string[i] == string[j]:
dp[i][j] = dp[i + 1][j - 1] + 2
else:
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
return dp[0][-1]
方案三:滚动数组
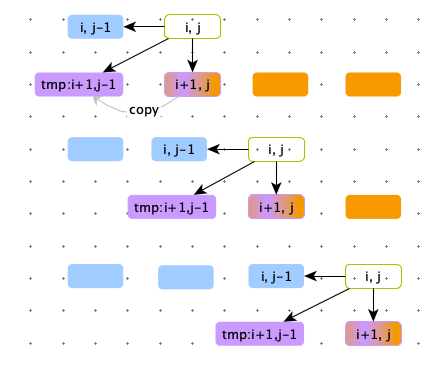
如图(i,j)依赖的左下方的数据,总是被覆盖,在覆盖前需要copy 到一个变量中 tmp:tmp = d[j]
tmp 初始化值根据上述矩阵可知 tmp = 0
def max_sub_palindrome3(string):
if not string: return 0
n = len(string)
dp = [1] * n
for i in range(n - 2, -1, -1):
tmp = 0
for j in range(i + 1, n):
if string[i] == string[j]:
new_value = tmp + 2
down = dp[j]
dp[j] = new_value
else:
new_value = max(dp[j], dp[j - 1])
tmp = dp[j]
dp[j] = new_value
return dp[-1]
上述三个方案只是求出最长回文子序列的长度。
方案四:动态规划:求最长的回文子序列
在计算完毕最长回文子序列的长度后,能够得到长度和 dp 表。我们可以根据 dp 表反推出最长回文子序列
- 如果 str[i] == str[j] ,i 和 j 跳到 左下边:i ++,j –
- 如果 str[i] != str[j] ,dp[i][j] 与左边或者下边的哪个值相等就跳到对应位置
上述规则可以求出其中一种答案,如果要求出所有答案,可以对 dp 进行深度遍历(dp[i][j] 与 左边和下边都相等,那么这两种情况都需要保留 )。
def max_sub_palindrome4(string):
if not string: return ""
n = len(string)
dp = [[0] * n for _ in range(n)]
# base case
for i in range(n):
dp[i][i] = 1
for i in range(n - 2, -1, -1):
for j in range(i + 1, n):
if string[i] == string[j]:
dp[i][j] = dp[i + 1][j - 1] + 2
else:
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
count = row = 0
col = n - 1
res_len = index = dp[row][col]
res = [None] * index
while count < res_len:
if row < n - 1 and dp[row][col] == dp[row + 1][col]:
row += 1
elif col > 0 and dp[row][col] == dp[row][col - 1]:
col -= 1
else:
index -= 1
res[res_len - index - 1] = res[index] = string[row]
count += 2
row += 1
col -= 1
return res
