模型集成

2024-10-09 | 阅读：次

模型集成

三个臭皮匠顶一个诸葛亮。

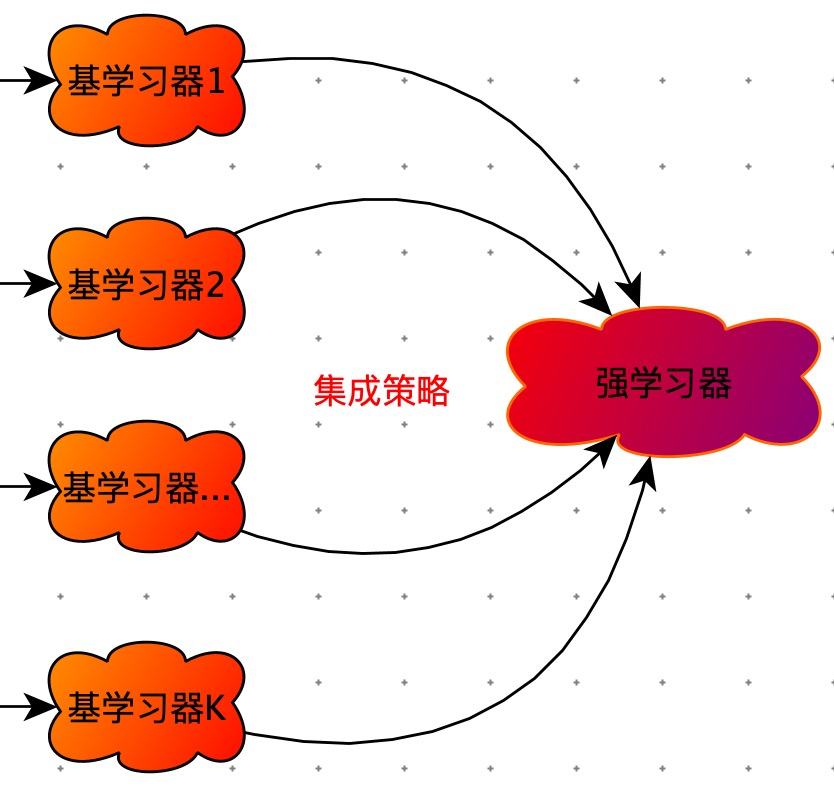
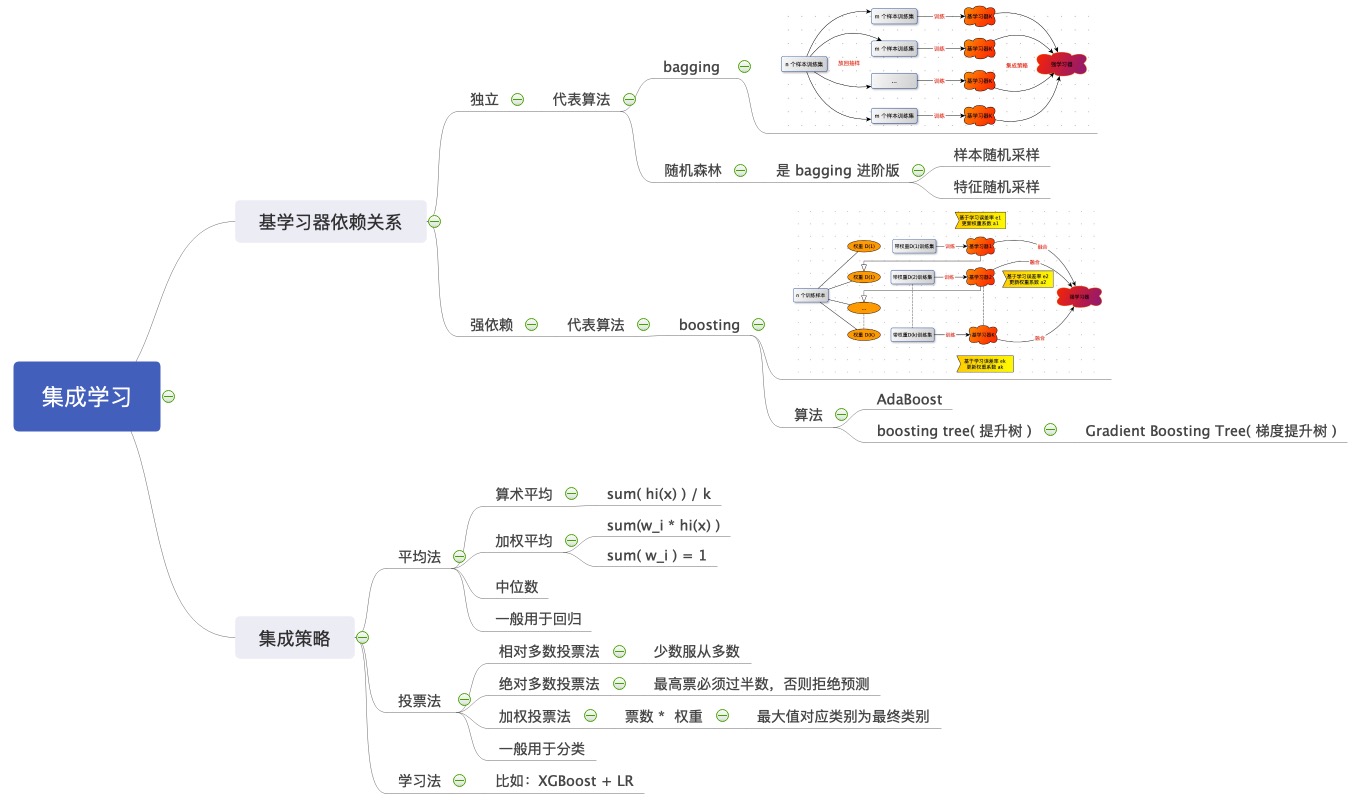
将多个模型融合在一起，得到一个单一模型。

应用：分类，回归，聚类，推荐…

为什么要集成？

结论：将多个模型融合会得到更好的精确度。

假设有 5 个 Accuracy = 70% 的分类器，相互独立。采用投票的方式将 5 个分类器的结果进行集成：当一个样本被三个及以上的分类器判断为正例，那么集成模型就判断为正例。

集成模型的精度为：$C_5^20.7^30.3^2+C_5^40.7^40.3^1+C_5^5*0.7^5=83.7\%$

如果是 101 个分类器（必须保证101个分类器**相互独立**,这个很难），那么 Accuracy = 99.9%

模型集成要解决的问题

如何获得多个模型，并且尽量相互独立。
如何将多模型的结果融合。

主要的集成思想

Committees：委员会，就是投票。每个模型都有投票权。
Boosting：贪心算法。如果要训练 n 个模型，每次训练一个模型，根据上一个模型训练的结果训练下一个模型。
Space split：将一个很大问题空间分割成 n 块，每次训练一个模型。比如：决策树
Mixture Model：空间软化分

Committees

多个模型的结果进行融合。

分类问题：投票。
回归问题：模型的输出的均值。

Bagging

解决问题：获得多个模型，并且尽量相互独立。也就是获取多个独立的训练集。可以并行训练模型。

Bagging（Bootstrap Aggregation）自举集成。

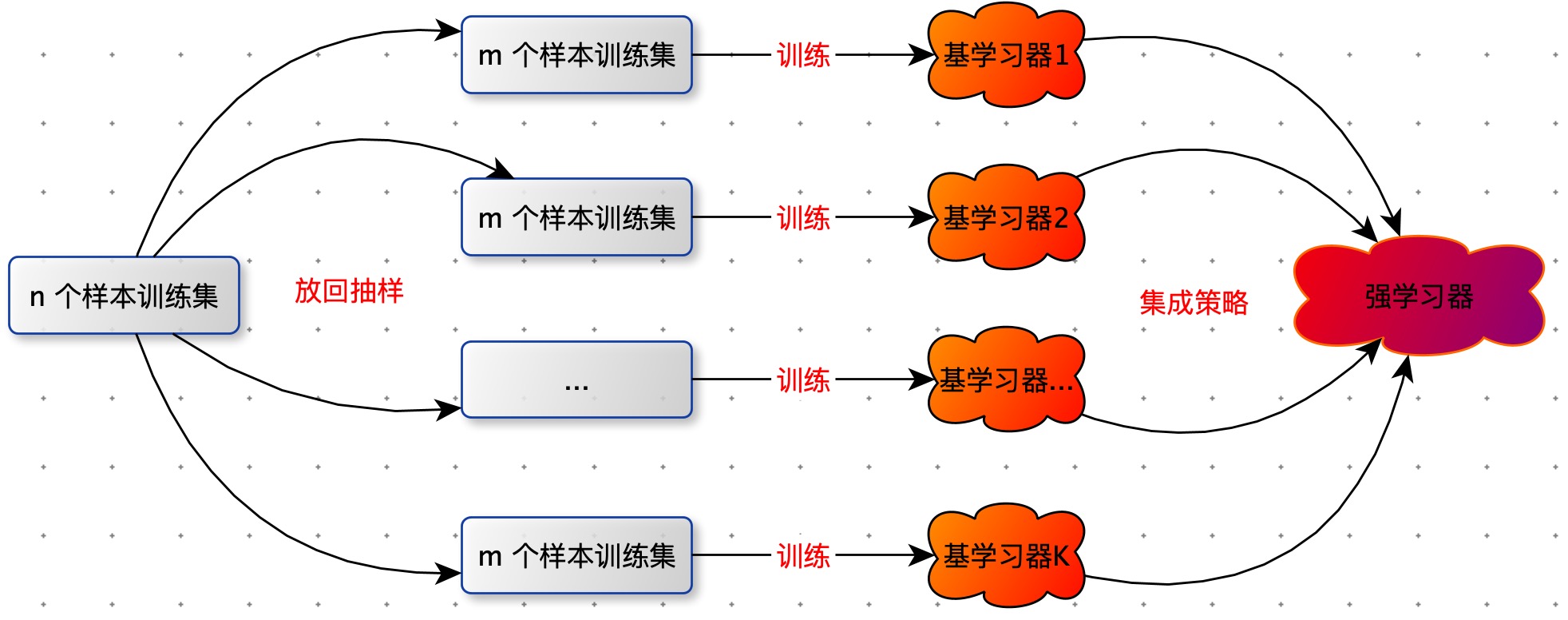
算法描述

对训练数据集进行**等概率放回采样**，得到多个训练数据集，分别训练模型。

带放回的采样概率分析：

训练集有 n 条样本，放回的随机抽出 n 个样本。问：每个样本被抽的概率是多少？

分析：

样本被抽到的概率：$\frac{1}{n}$

样本被没抽到的概率：$1-\frac{1}{n}$

n 次抽样都被没抽到的概率：$(1-\frac{1}{n})^n$

n 次抽样都至少一次被抽到的概率：$1-(1-\frac{1}{n})^n$

当 n 很大时：$limit_{n\rightarrow$ }{1-(1-\frac{1}{n})^n}=1-\frac{1}{e}=0.632$

Bagging 特点

Bagging 适合弱分类器

不稳定：随机采样会得到不同的基分类器。
每个基分分类器准确率略高于 50%。
Bagging较适合偏差小，方差大的基分类器（决策树）。

Bagging 不适合强分类器

每个基分类器只有更少的训练样本，集成后反而不如单个分类器。

Boosting

核心思想：对训练数据集进行采样，当前分错的样本采样权重更大。

Boosting 工作机制：

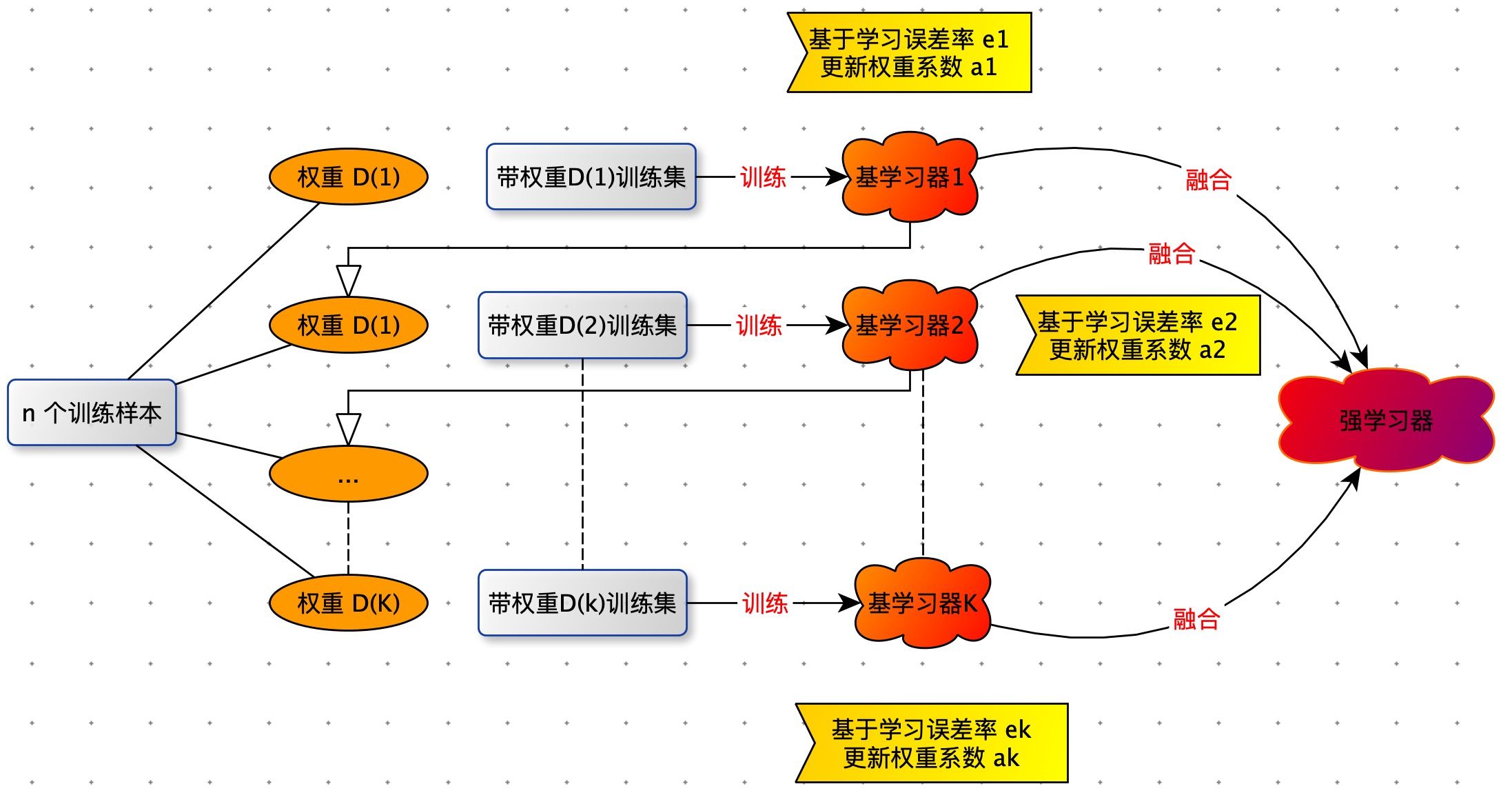
迭代 k 次，得到 k 个模型。

多模型融合：不等权投票，加大误差率小的分类器的投票权重。

AdaBoost

解决问题：通过不同权重的重采样获取不过训练集。必须顺序训练模型。

算法过程

假设是一个二分类任务。

输入：训练集 $T=[(x_1,y_1),(x_2,y_2),…,(x_n,y_n)]\,\,; x_i \in X \subseteq R^n\,;y_i \in Y=[-1,1]$

输出：G(x)

初始化训练数据的权值分布（等权）：

$D_1=(w_{1,1},w_{1,2},…,w_{1,i},…,w_{1,n}) \,;w_{1,i}=\frac{1}{N},i = 1,2,…,N$
根据样本的权重，有放回抽样，进行 M 轮，得到 M 个模型。
1. 在 $D_m$ 上，训练出一个基分类器：$G_m(x):X\rightarrow [-1,+1]$
2. 计算$G_m(x) $在训练集 $D_m$ 上的分类误差率：$e_m = P(G_m(x_i)!=y_i)=\sum_{i-1}^N{w_{mi}I(G_m(x_i)!=y_i)}$
  注意：加权分类误差率
  $w_{mi}$
3. 计算$G_m(x)$ 的系数（模型的权重）：$a_m = \frac{1}{2}log_e{\frac{1-e_m}{e_m}}$
4. 更新训练数据的权值分布：$D_{m+1}=(w_{m+1,1},w_{m+1,2},…,w_{m+1,i},…,w_{m+1,n})$
  
  $w_{m+1,i} = \frac{w_{m,i}}{Z_m}e^{-a_my_iG_m(x_i)};i=1,2,…,N$
  
  $Z_m$规范化因子：$Z_m=\sum_{i=1}^Nexp(-a_my_iG_m(x_i))$
  
  $Z_m$ 使 $D_m$ 成为一个分布。
构建基本分类器的线性组合：$f(x)=\sum_{i=1}^M{a_mG_m(x)}$

最终分类器：$G(x)=sign(f(x))=sign(\sum_{i=1}^M{a_mG_m(x_i)})$

def ada_boost_train(data_set, label, num=40):
    class_list = []
    n = len(data_set)
    w = [1.0 / n] * n
    agg_class_est = [0.0] * n

    for i in range(num):
        # 构建基分类器：决策树
        best_stump, error, class_est = build_stump(data_set, label, w)

        alpha = float(0.5 * math.log((1.0 - error) / error, math.e))
        best_stump["alpha"] = alpha
        class_list.append(best_stump)

        print("alpha=%s, classEst=%s, bestStump=%s, error=%s " % (alpha, class_est, best_stump, error))

        expon = [0.0] * n
        for i in range(n):
            expon[i] = -1 * alpha * label[i] * class_est[i]

        for i in range(n):
            w[i] = w[i] * math.e(expon[i])

        z = sum(w)
        w = [w_i / z for w_i in w]

        agg_class_est = [agg_class_est[i] + alpha * class_est[i] for i in range(n)]
    return class_list, agg_class_est

GBDT

Gradient Boosting Decision Tree，梯度提升决策树。

GBDT 的基分类器限定只能是：CART 回归树模型。

每一次对残差（实际值与预测值之差）进行拟合，最后把预测值相加得到最终的预测值。

比如：灯泡的寿命是10年，经过三棵树的训练（拟合10），第一颗树的训练结果为 5 年，那么残差为10-5=5年，在此基础上训练（拟合10 - 5 =5），第二棵树的训练结果为 3 年，残差为5-3=2年，接着第三棵树（拟合5 - 3 =2），训练结果为1年，残差为2-1=1年，结束，那么这棵树最终预测的寿命=5+3+1=9年，这个结果显然更接近于真实值。

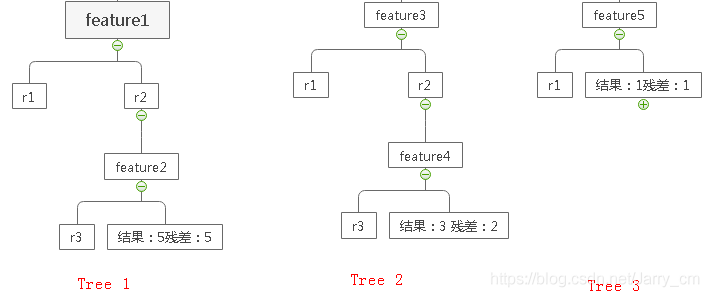
残差拟合思想蛮简单，但是损失的拟合不好度量。

负梯度拟合

通过梯度提升的方法集成多个决策树。

大牛Freidman提出了用损失函数的负梯度来拟合本轮损失的近似值，进而拟合一个CART回归树。

通过损失函数的负梯度来拟合，我们找到了一种通用的拟合损失误差的办法，这样无论是分类问题还是回归问题，我们通过其损失函数的负梯度的拟合，就可以用GBDT来解决我们的分类回归问题。区别仅仅在于损失函数不同导致的负梯度不同而已。

加法模型

$y_i = \sum_{k=1}^K{f_k(x_i)},f_k \in F$

如何学习加法模型？

前向分布算法（forward stagewise algorithm），因为学习的是加法模型，如果能够从前往后，每一步只学习一个基函数及其系数（结构），逐步逼近优化目标函数，那么就可以简化复杂度。这一学习过程称之为 Boosting。

例如：

决策树的复杂度可以由正则项

$\Omega(f_t) = r*T+\frac{1}{2}\lambda \sum_{j=1}^T{w_j^2} $

T：树的叶子节点数量
w：叶子节点对应的值向量的 L2 范数

节点分裂收益

假设当前节点为 C ，分裂后左孩子节点为 L，右孩子节点为 R。obj 为目标函数值。

$Gain = obj_c - obj_L - obj_R$

$Gain = \frac{1}{2}[\frac{G_L^2}{H_L+\lambda} +\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda} ] - r$

$-r$ 表示：因为增加了树的复杂性（该分裂增加了一个叶子节点）带来的惩罚。

参考：https://cloud.tencent.com/developer/article/1005611

XGBoost

XGBoost是一种集成学习算法，通过CART 回归树，每一次对残差（实际值与预测值之差）进行拟合，最后把预测值相加得到最终的预测值。

XGBoost 中树都是二叉树。

XGBoost 特点

w 是最优化求出来的，不是平均值或规则指定的，这是XGBoost的一个创新。
loss function中包含了正则化防止过拟合的技术。
支持自定义loss function，只要能泰勒展开（能求一阶导和二阶导）就行。
支持并行化，训练速度快，boosting技术中下一棵树依赖上述树的训练和预测，所以树与树之间应该是只能串行！但是在选择最佳分裂点，进行枚举的时候并行！（这个也是树形成最耗时的阶段）。
XGBoost还特别设计了针对稀疏数据的算法。
可实现后剪枝
交叉验证，方便选择最好的参数
行采样、列采样，随机森林的套路（防止过拟合）。
预测值为每个回归树预测值的加和，这里也可以是加权。
XGBoost还支持设置样本权重，这个权重体现在梯度g和二阶梯度h上，是不是有点adaboost的意思，重点关注某些样本。

XGBoost 参数

通用参数

n_estimators：
booster ：默认值 gbtree。

选择基模型，gbtree：树模型，gbline：线性模型。
Silent ：默认值为 0。

Silent = 1静默模式开启，不会输出任何日志。0 帮助我们了解模型运行情况。
nthread：默认值最大可能的线程数。

多线程的控制，应当输入系统的核数。如果希望使用cpu 全部核，就不要输入这个参数，算法会自动检测。

booster 参数

eta[默认是0.3] 和GBM中的learning rate参数类似。通过减少每一步的权重，可以提高模型的鲁棒性。典型值0.01-0.2
min_child_weight[默认是1] 决定最小叶子节点样本权重和。当它的值较大时，可以避免模型学习到局部的特殊样本。但如果这个值过高，会导致欠拟合。这个参数需要用cv来调整
max_depth [默认是6] 树的最大深度，这个值也是用来避免过拟合的3-10
max_leaf_nodes 树上最大的节点或叶子的数量，可以代替max_depth的作用，应为如果生成的是二叉树，一个深度为n的树最多生成2n个叶子,如果定义了这个参数max_depth会被忽略
gamma[默认是0] 在节点分裂时，只有在分裂后损失函数的值下降了，才会分裂这个节点。Gamma指定了节点分裂所需的最小损失函数下降值。这个参数值越大，算法越保守。
max_delta_step[默认是0] 这参数限制每颗树权重改变的最大步长。如果是0意味着没有约束。如果是正值那么这个算法会更保守，通常不需要设置。
subsample[默认是1] 这个参数控制对于每棵树，随机采样的比例。减小这个参数的值算法会更加保守，避免过拟合。但是这个值设置的过小，它可能会导致欠拟合。典型值：0.5-1
colsample_bytree[默认是1] 用来控制每颗树随机采样的列数的占比每一列是一个特征0.5-1
colsample_bylevel[默认是1] 用来控制的每一级的每一次分裂，对列数的采样的占比。
lambda[默认是1] 权重的L2正则化项
alpha[默认是1] 权重的L1正则化项
scale_pos_weight[默认是1] 各类样本十分不平衡时，把这个参数设置为一个正数，可以使算法更快收敛。

学习目标参数

Objective：默认值 reg:linear

这个参数定义需要被最小化的损失函数。最常用的值有：binary：logistic二分类的逻辑回归，返回预测的概率非类别。multi:softmax使用softmax的多分类器，返回预测的类别。在这种情况下，你还要多设置一个参数：num_class类别数目。
eval_metric：默认值取决于objective参数的取值。

对于有效数据的度量方法。对于回归问题，默认值是rmse，对于分类问题，默认是error。典型值有：rmse均方根误差；mae平均绝对误差；logloss负对数似然函数值；error二分类错误率；merror多分类错误率；mlogloss多分类损失函数；auc曲线下面积。
seed：默认是 0

随机数的种子，设置它可以复现随机数据的结果，也可以用于调整参数。

模型保存

# 初始化 xgboost 实例
XGB = xgb.XGBClassifier(n_estimators=100, objective="binary:logistic")
# 训练
XGB.fit(x_train, y_train)    
# 保存模型
# 模型文件位置
XGB.get_booster().dump_model("/Users/dongyf/dongyf/data/status_rank/model.txt",fmap='/Users/dongyf/dongyf/data/status_rank/tmp_fmap')

fmap ：指定导出模型的特征名。

fmap 的文件格式（以空分隔）：共三列

Feature_id featrue_name (q or i or int)

feature_id：从 0 开始直到特征的个数为止，从小到大列。
Feature_name：model 要指定的 name
第三列
- q 表示是数字特征，可以省略 int 表示特征为整数
- i 表示是二分类特征

fmap 文件

user_stock_score q
status_uid q
time q
allSymbolsCharLength q
allSymbolsSize q
contentLength q
favCount q
followerCount q
likeCount q
replyCount q
retweetCount q
staticScore q
symbolAccessOrde q

模式为：

booster[0]:
0:[replyCount<3.5] yes=1,no=2,missing=1
        1:[staticScore<16.7780495] yes=3,no=4,missing=3
                3:[status_uid<1.00048115e+09] yes=7,no=8,missing=7
                        7:[time<61080400] yes=15,no=16,missing=15
                                15:[time<60873856] yes=31,no=32,missing=31
                                        31:[contentLength<47.5] yes=61,no=62,missing=61
                                                61:leaf=-0.491739154
                                                62:leaf=-0.554545462
                                        32:[time<60969072] yes=63,no=64,missing=63
                                                63:leaf=-0.0666666701
                                                64:leaf=0.150000006
                                16:leaf=-0.565105617
                        8:[staticScore<10.0133038] yes=17,no=18,missing=17
                                17:[status_uid<1.00948416e+09] yes=33,no=34,missing=33
                                        33:[time<19740952] yes=65,no=66,missing=65
                                                65:leaf=0.150000006
                                                66:leaf=-0.163636371
                                        34:[favCount<20.5] yes=67,no=68,missing=67
                                                67:leaf=-0.530347824
                                                68:leaf=-0.47329843
                                18:[contentLength<13.5] yes=35,no=36,missing=35
                                        35:[contentLength<12.5] yes=69,no=70,missing=69
                                                69:leaf=-0.443478286
                                                70:leaf=-0.0923077017
                                        36:[time<462659840] yes=71,no=72,missing=71
                                                71:leaf=-0.498947412
                                                72:leaf=-0.272727281

参考：https://blog.csdn.net/Jarry_cm/article/details/104279528

见路不走

董一峰

模型集成

目录

模型集成

为什么要集成？

模型集成要解决的问题

主要的集成思想

Committees

多个模型的结果进行融合。

Bagging

Bagging 特点

Boosting

AdaBoost

算法过程

GBDT

负梯度拟合

XGBoost

XGBoost 参数

通用参数

booster 参数

学习目标参数

模型保存