旋变字符串

2022-11-04 | 阅读：次

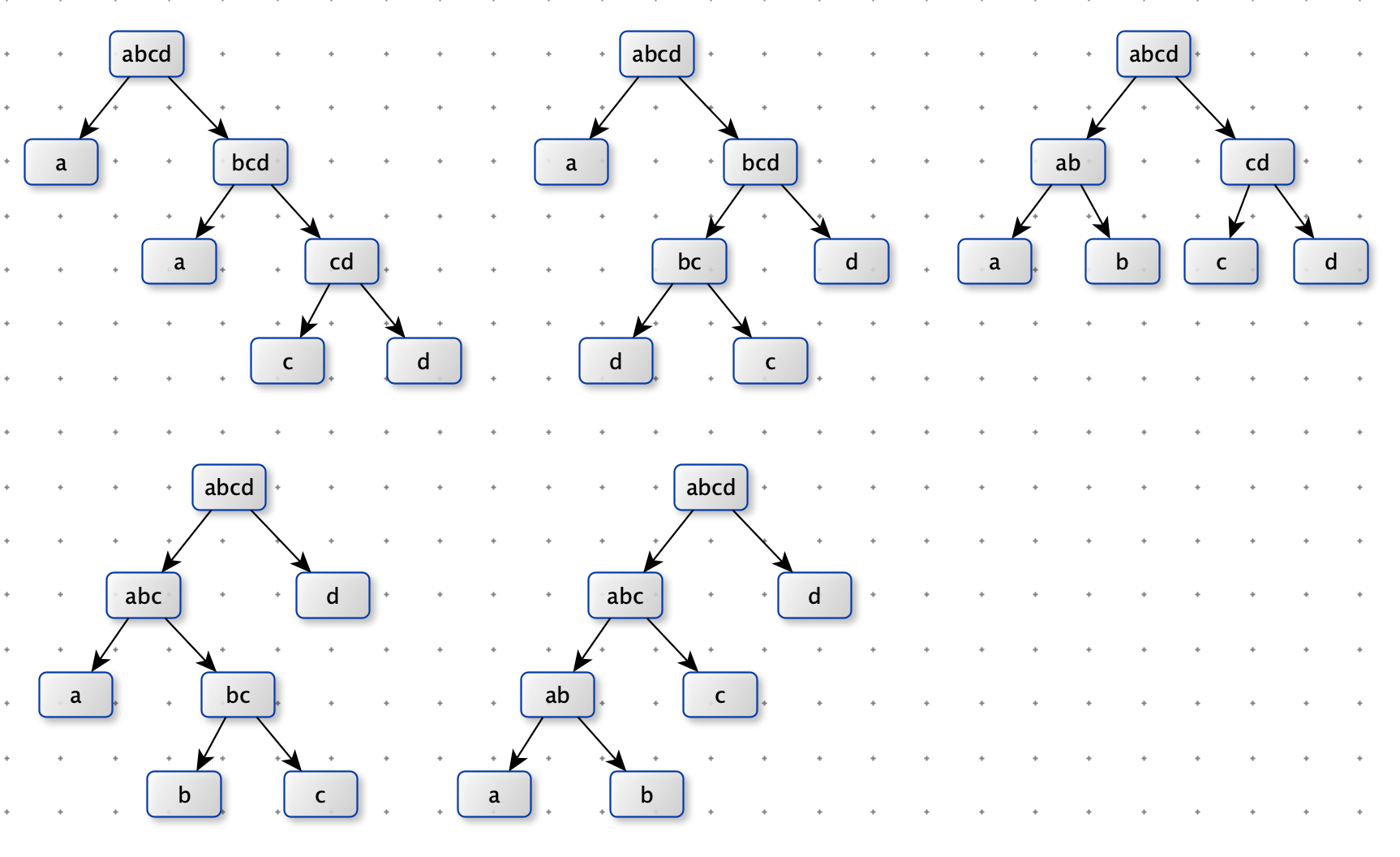
一个字符串可以分解成多种二叉树结构。如果 str 长度为 1 ，认为不可分解。如果 str 长度为 N（N > 1）,左部分长度可以为 1 ~ N - 1，剩下的为右部分的长度。左部分和右部分都可以按照同样的逻辑，继续分解。形成的所有结构都是 str 的二叉树结构。

比如，字符串“abcd”，可以分解成一下五种结构：

任何一个str的二叉树结构中，如果两个节点有共同的父节点，那么这两个节点可以交换位

置，这两个节点叫作一个交换组。一个结构会有很多交换组，每个交换组都可以选择进行交

换或者不交换，最终形成一个新的结构，这个新结构所代表的字符串叫作 str的旋变字符串。

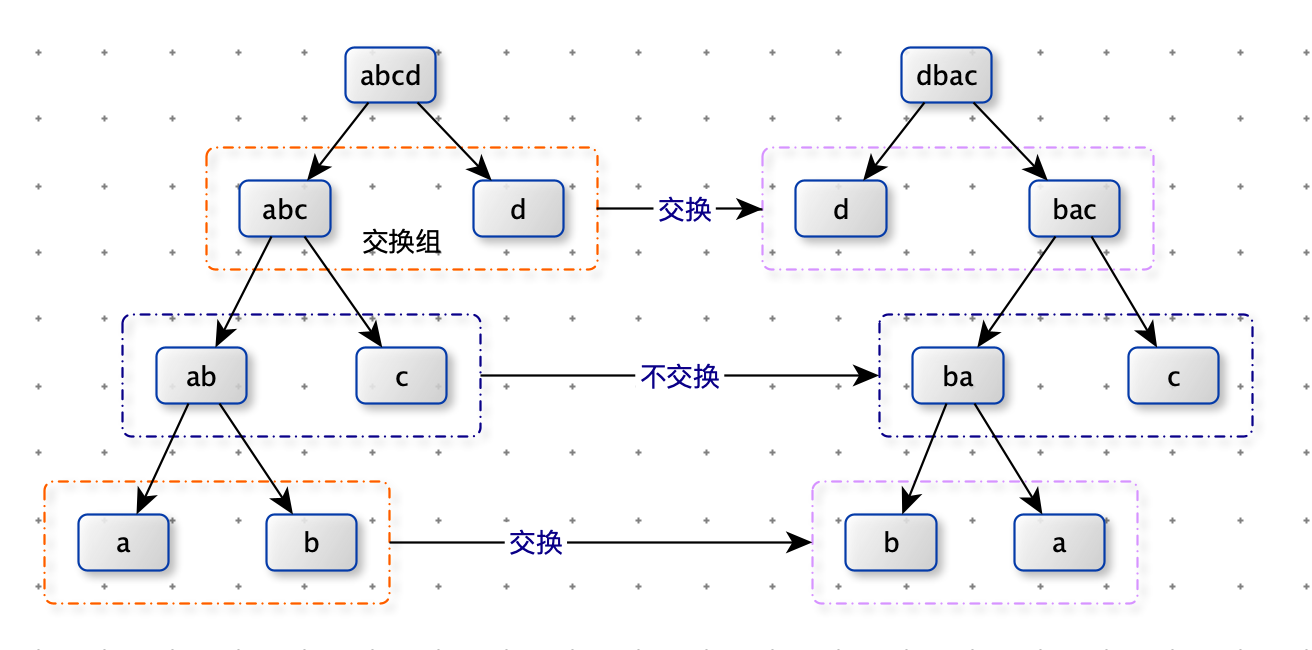
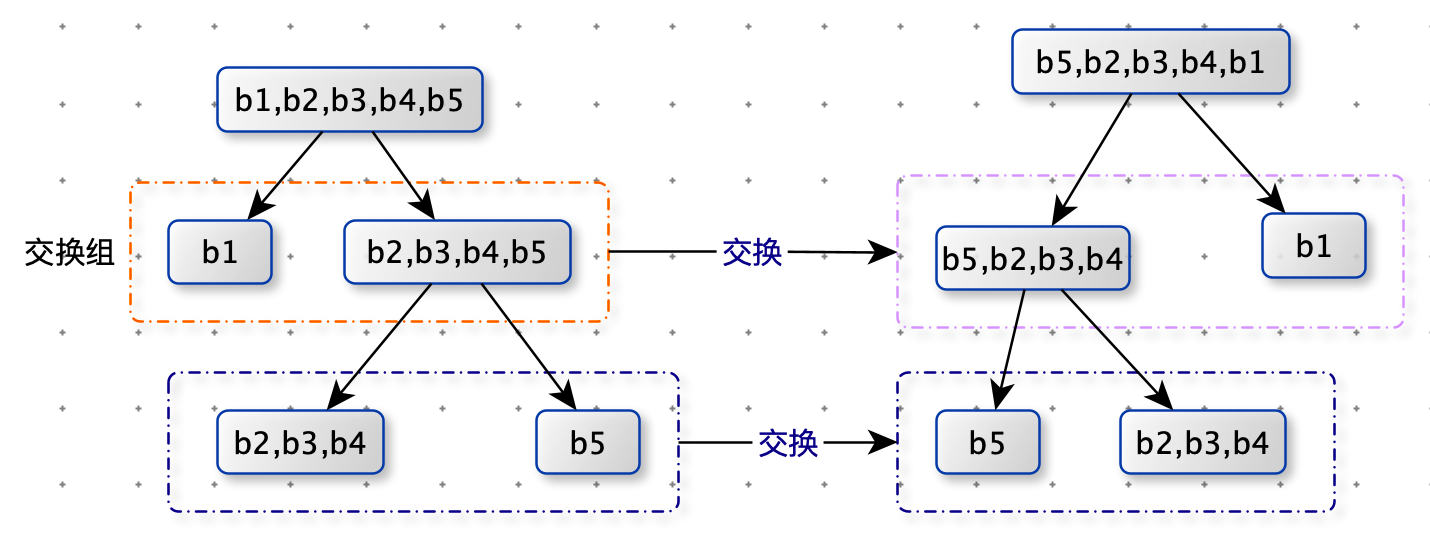
比如，在上面的结构五中，交换组有a和b、ab和c、abc和d。如果让a和b的组交换；让ab和

c的组不交换；让abc和d的组交换，形成的结构如图

这个新结构所代表的字符串为”dbac”，叫作”abcd”的旋变字符串。也就是说，一个字符串

str的旋变字符串是非常多的，str 可以形成很多种结构，每一种结构都有很多交换组，每

一个交换组都可以选择交换或者不交换，形成的每一个新的字符串都叫 str的旋变字符串。

给定两个字符串str1和str2，判断str2是不是str1的旋变字符串。

解法一：暴力递归

分析：

str2 是 str1 的旋变字符串必须满足一下条件：

len( str1 ) == len( str2 )
str1 和 str2 的字符种类必须相同。
str1 和 str2 的每种字符的个数必须相同。

根据以上三个条件，我们可以写一个过滤器。

def valid(str1, str2):
    if len(str1) != len(str2): return False

    map1 = {}
    for i in range(len(str1)):
        map1[str1[i]] = map1.get(str1[i], 0) + 1

    for i in range(len(str2)):
        num = map1.get(str2[i], 0)
        num -= 1
        if num < 0: return False
        map1[str2[i]] = num

    return True

尝试模型是：范围上尝试

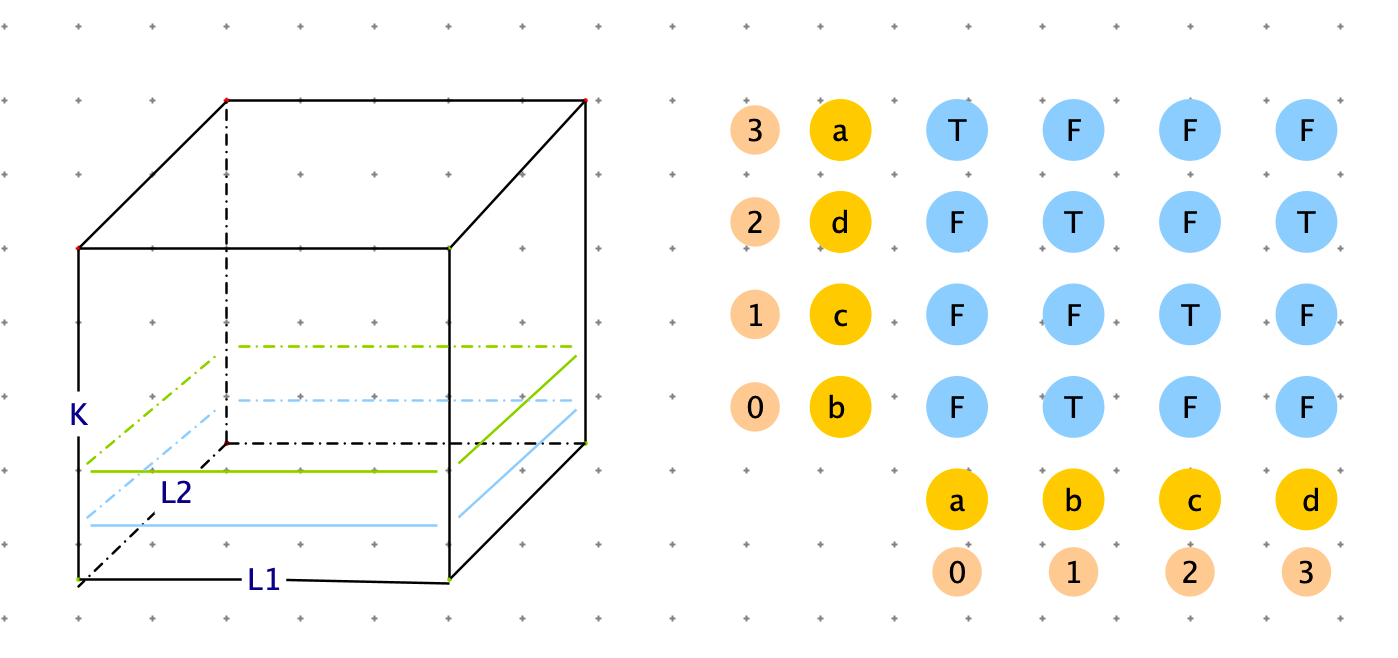
判断 $str[L_1…R_1]$ 和 $str[L_2…R_2]$ 是不是互为旋变字符串。

此种尝试方案：有四个参数：$L_1,R_1,L_2,R_2$

根据上边过滤器的条件，我们知道 $str[L_1…R_1]$ 和 $str[L_2…R_2]$ 要是互为旋变字符串，长度必须相等。因此，我们可以将将参数压缩成三个：$L_1,L_2,K$ ，k 是str1 的长度。

$f(L_1,L_2,K)$ 表示判断 $str[L_1…K+L_1]$ 和 $str[L_2…K+L_2]$ 是不是互为旋变字符串。

最终返回结果：f( 0, 0, len(arr) - 1)

Base case

如果 k ==1 只有一个字符，只要 $str1[L_1]= str2[L_2]$

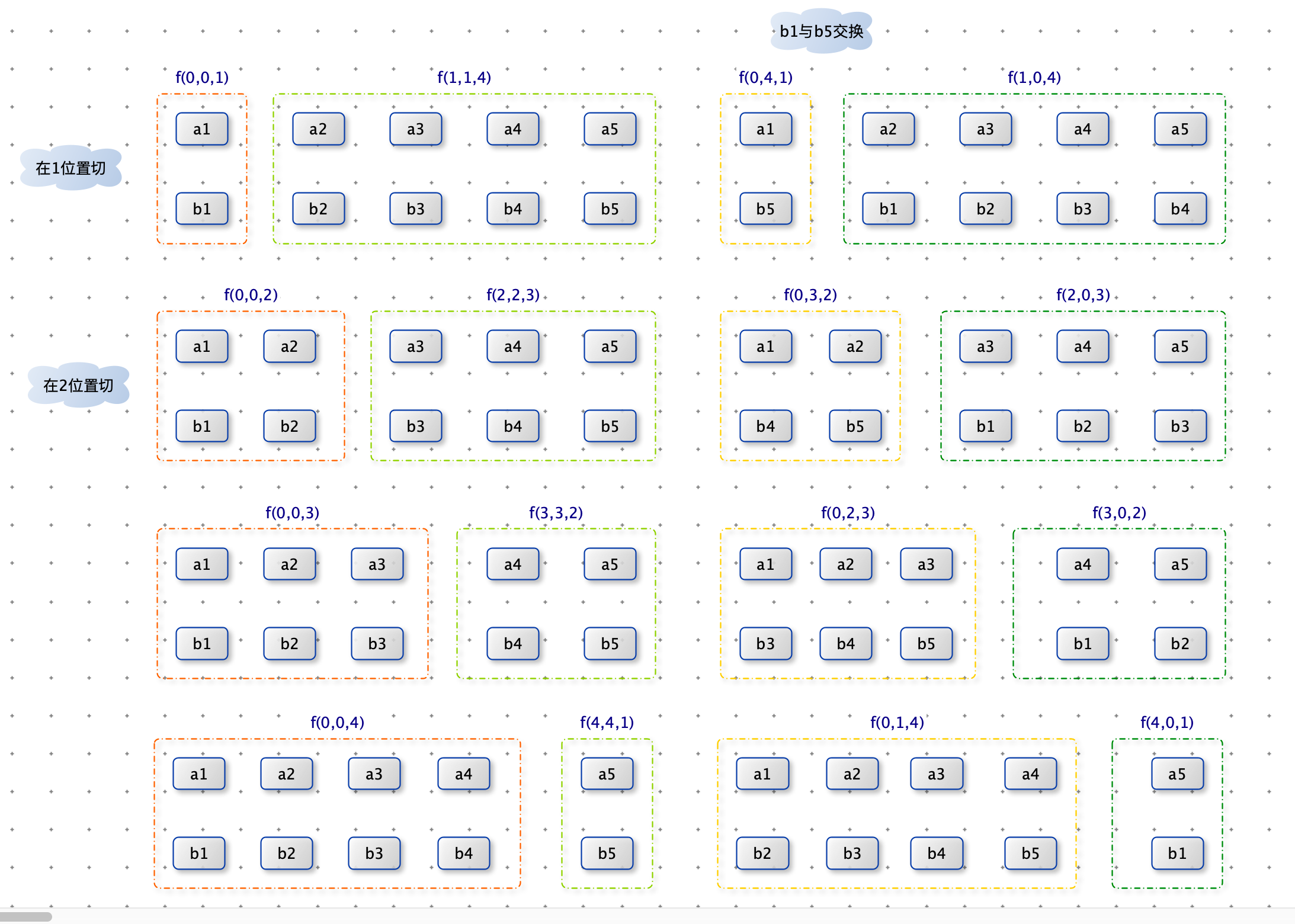
如下图：第一刀在 str 中每一个位置进行尝试，每一刀分隔出的两部分进行比对（调用子过程），需要交换后再比对（调用子过程）。

只要有一部分是互为旋变字符串，就返回true。否则继续尝试第二刀，第三刀…

def is_scramble(str1, str2):
    if not str1 and not str2: return True
    if (not str1 and str2) or (str1 and not str2): return False
    if str1 == str2: return True
    if not valid(str1, str2): return False
    return f(str1, str2, 0, 0, len(str1))

def f(str1, str2, l1, l2, k):
    if k == 1: return str1[l1] == str2[l2]

    for i in range(1, k):
        res = (f(str1, str2, l1, l2, i) and f(str1, str2, l1 + i, l2 + i, k - i)) or \
              (f(str1, str2, l1, l2 + k - i, i) and f(str1, str2, l1 + i, l2, k - i))
        if res: return True

    return False

解法二：动态规划

$k \in (1,n] $
$L_1,L_2 \in(0,n)$

本地依赖关系不好梳理，但是原问题的 k ，和依赖的子问题的 k’ 的关系是：k‘ < k。所以在填充当前层数据时，只依赖下边层的数据，不依赖本次层数据。dp 表填充顺序，从下向上填写。

base case 是 k ==1 时，$dp[1][l_1][l_2] = str1[l_1] == str2[l_2]$

def is_scramble2(str1, str2):
    if not str1 and not str2: return True
    if (not str1 and str2) or (str1 and not str2): return False
    if str1 == str2: return True
    if not valid(str1, str2): return False

    n = len(str1)
    dp = []
    for i in range(n + 1):
        dp.append([[False] * n for _ in range(n)])

    for l1 in range(n):
        for l2 in range(n):
            dp[1][l1][l2] = str1[l1] == str2[l2]

    for k in range(2, n + 1):
        for l1 in range(0, n - k + 1):
            for l2 in range(0, n - k + 1):
                for i in range(1, k):
                    if (dp[i][l1][l2] and dp[k - i][l1 + i][l2 + i]) or \
                            (dp[i][l1][l2 + k - i] and dp[k - i][l1 + i][l2]):
                        dp[k][l1][l2] = True
                        break

    return dp[n][0][0]

见路不走

董一峰

旋变字符串

目录