给定一个数组 arr,代表一排有分数的气球。每打爆一个气球都能获得分数,假设打爆气球的分数为 X,获得分数的规则如下:
- 如果被打爆气球的左边有没打爆的气球,找到离被打爆气球最近的气球,假设分数为 L;如果被打爆气球的右边有没有打爆的气球,找到离被打爆气球最近的气球,假设分数为 R。获得分数为 L * X * R
- 如果被打爆气球的左边有没打爆的气球,找到离被打爆气球最近的气球,假设分数为 L;如果被打爆气球的右边所有气球都已经被打爆。获得分数为:L*X
- 如果被打爆气球的左边所有气球都已经被打爆;如果被打爆气球的右边有没有打爆的气球,找到离被打爆气球最近的气球,假设分数为 R。获得分数为:R*X
- 如果被打爆气球的左边和右边所有气球都已经被打爆。获得分数为:X
目标是打爆所有气球,返回能获得的最大分数。
【举例】
arr =【3,2,5】
- 如果先打爆 3,获得 3*2;再打爆 2,获得 2* 5 ;最后打爆 5 ,获得 5;总分为:6+10+5=21.
- 如果先打爆 3,获得 3*2;再打爆 5,获得 2* 5 ;最后打爆 2 ,获得 2;总分为:6+10+2=18.
- 如果先打爆 2,获得 3*2*5;再打爆 3,获得 3* 5 ;最后打爆 5 ,获得 5;总分为:30+15+5=50.
- 如果先打爆 2,获得 3*2*5;再打爆 5,获得 3* 5 ;最后打爆 3 ,获得 3;总分为:30+15+3=48.
- 如果先打爆 5,获得 2*5;再打爆 3,获得 3* 2 ;最后打爆 2 ,获得 2;总分为:10+6+2=18.
- 如果先打爆 5,获得 2*5;再打爆 2,获得 3* 2 ;最后打爆 3 ,获得 3;总分为:10+6+3=19.
返回最大分数为 50
本题练习:尝试方案选择技巧。
解法一:暴力递归
可能性分析:
范围尝试模型。
尝试方案一
尝试每一个位置的气球**优先**被打爆。
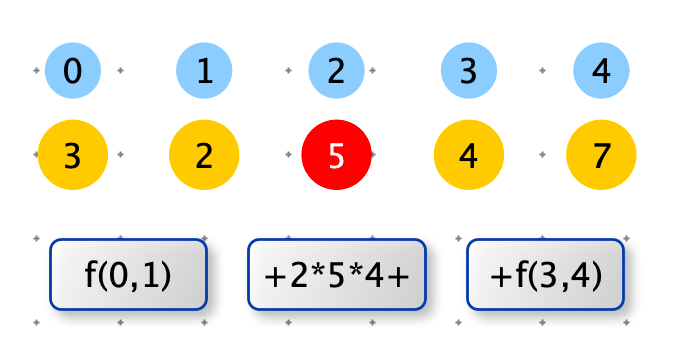
例如:下图先打爆下标为 2 的气球,那么左边的子过程是:f(0, 1) 。由于下标为 2 的气球已经被打爆,因此 f(0,1) 无法确定右边没有打爆最近的气球。同理f(3, 4) 无法确定左边没有打爆最近的气球。
因此需要其他参数来供子问题决策。f( left , right, left_score, right_score),left_score 表示左边没有打爆的最近气球。right_score 表示右边有没有打爆的最近气球。
f 有四个变量,在改动态规划时,需要一张四维表,并且这张四维表的大小受限于 arr 中数值的大小。
结论:这种尝试模型不够好。
尝试方案二
尝试每一个位置的气球**最后**被打爆。
f(L , R) 表示打爆 arr[L…R] 上所有的气球。
潜台词:L - 1 和 R + 1 的气球一定没有被打爆。
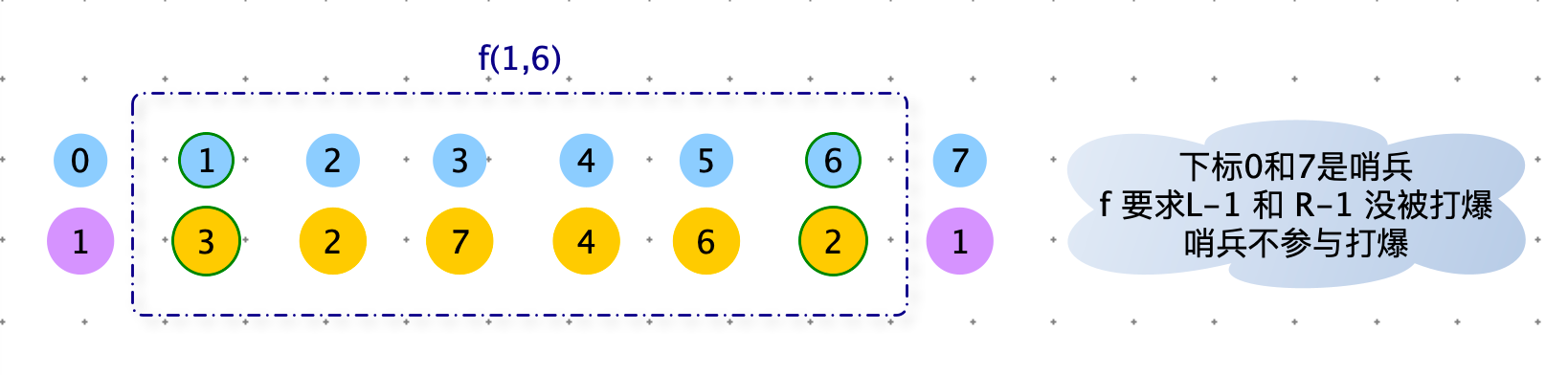
如下图:f(1, 6) 需要将下标从 1 到 6 的气球逐一尝试最后打爆。两个端点 1 和 6 计算比较特殊,单独计算一下。
f(1,1) 表示下标 1 最后被打爆,那么其他气球(2,3,4,5,6)都已经被打爆了,所以 $f(1,1)=arr[0]arr[1]arr[7]$
同理:$f(1,1)=arr[0]arr[6]arr[7]$
对于中间下边比如:下标 2 最后被打爆,那么其他气球已经被打爆(1,3,4,5,6),气球 1 被打爆:f(1,1) 和 气球 3,4,5,6 被打爆表示为 f(3,6) 。因此 $f(1,6)=f(1,1)+f(3,6)+arr[0]arr[2]arr[7]$
总结:此方案只需要两个参数,在改动态规划时,需要一张二维表。此方案比较优秀。
def max_score1(arr):
if not arr: return 0
# 哨兵,因为 f 要求 arr[l-1] 和 arr[r+1] 一定没有被打破
arr.insert(0, 1)
arr.append(1)
return f1(arr, 1, len(arr) - 2)
# 打爆 arr[l...r] 范围上的所有气球,返回最大的分数
# 假设arr[l-1] 和 arr[r+1] 一定没有被打破
def f1(arr, l, r):
# 如果 arr[l...r] 范围上只有一个气球,直接打爆即可
if l == r:
return arr[l - 1] * arr[l] * arr[r + 1]
# 最后打爆 arr[l] 的方案 和 最后打爆 arr[r] 的方案,先比较一下
res = max(arr[l - 1] * arr[l] * arr[r + 1] + f(arr, l + 1, r),
arr[l - 1] * arr[r] * arr[r + 1] + f(arr, l, r - 1))
# 尝试中间位置的气球最后打爆的每一种方案
for k in range(l + 1, r):
res = max(res, arr[l - 1] * arr[k] * arr[r + 1] + f(arr, l, k - 1) + f(arr, k + 1, r))
return res
总结:
- **大问题所有的影响都要通过参数传递给小问题,便于小问题在决策过程中使用。**
- **可能性尝试策略:递归函数参数越少越好,参数简单越好。**
解法二:动态规划
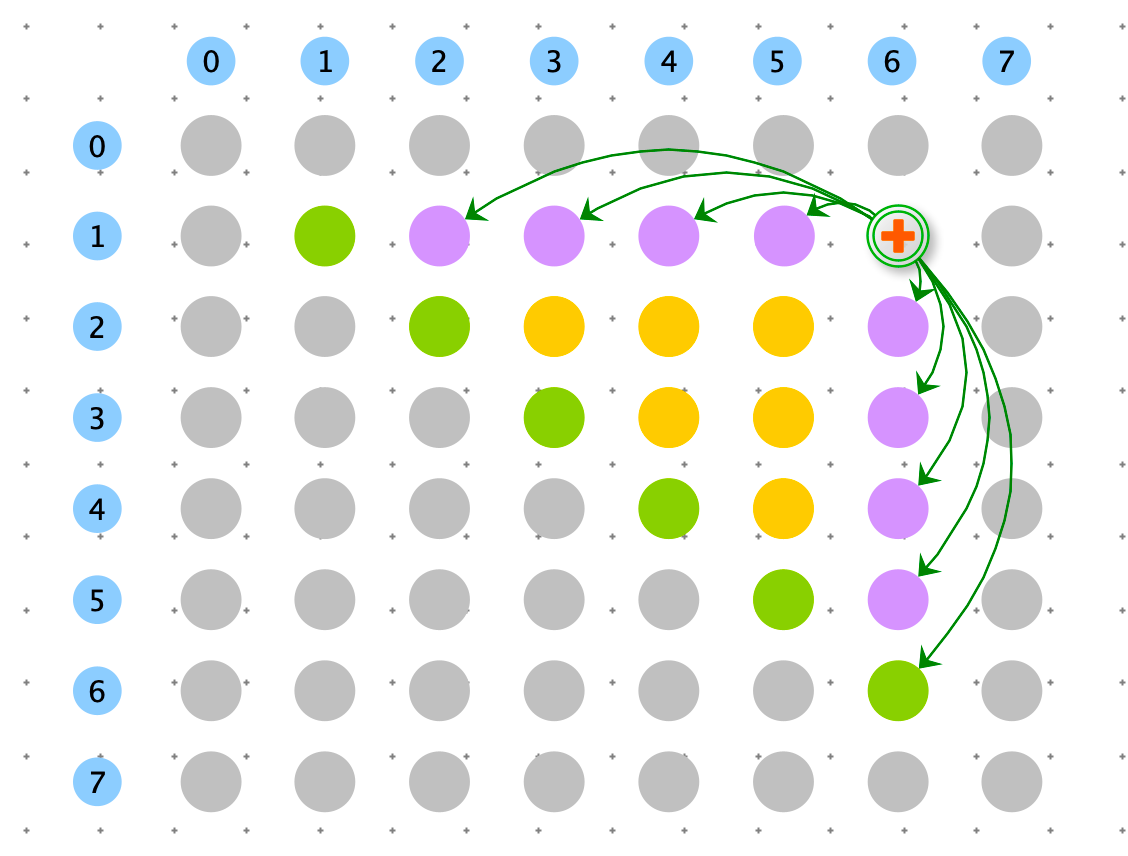
如下图:f(1, 6) 依赖 f(2 ,6), f(3,6), f(4,6), f(5,6), f(6,6), f(1 ,5), f(1,4), f(1,3), f(1,2)
def max_score2(arr):
if not arr: return 0
arr.insert(0, 1)
arr.append(1)
dp = [[0] * (len(arr)) for _ in range(len(arr))]
for i in range(1, len(arr) - 1):
dp[i][i] = arr[i - 1] * arr[i] * arr[i + 1]
for l in range(len(arr) - 3, 0, -1):
for r in range(l + 1, len(arr) - 1):
res = max(arr[l - 1] * arr[l] * arr[r + 1] + f(arr, l + 1, r),
arr[l - 1] * arr[r] * arr[r + 1] + f(arr, l, r - 1))
for k in range(l + 1, r):
res = max(res, arr[l - 1] * arr[k] * arr[r + 1] + f(arr, l, k - 1) + f(arr, k + 1, r))
dp[l][r] = res
return dp[1][len(arr) - 2]
对数器:
import random
def generator_random_arr(max_size, max_value):
return [item for item in
set([int(random.random() * max_value) + 1 for _ in range(int(random.random() * max_size) + 1)])]
def check():
global map
max_size = 5
max_value = 10
for _ in range(10000):
arr = generator_random_arr(max_size, max_value)
# print("info2", aim, arr)
res = max_score(arr[:])
res2 = max_score2(arr[:])
# print("Info", "res=", res, "res2=", res2, aim, arr)
if res != res2 or res != res2:
print("ERROR", "res=", res, "res2=", res2, arr)
print("OVER")
