一条直线上有 n 个线段,第 i 个线段的坐标为$(x_1[i],x_2[i])$。请你计算出直线上重叠线段数量最多的地方,有多少个线段相互重叠?
分析:
首先需要根据线段的起始点排序,便于后续处理。
线段重叠问题需要根据当前线段的 start 和 end 排除哪些没有重合的线段。
我们可以将线段的 end ,放入一个有序表里,将有序表中小于 start 的数据都删除(那些已加入有序表线段的 end 小于当前线段的 start,肯定与当前线段不重叠)。有序表中所有end 个数就是线段相互重叠数(由于 end 有可能重复,而有序表的 key 不能重复,所有用有序表 value 作为 end 个数)。
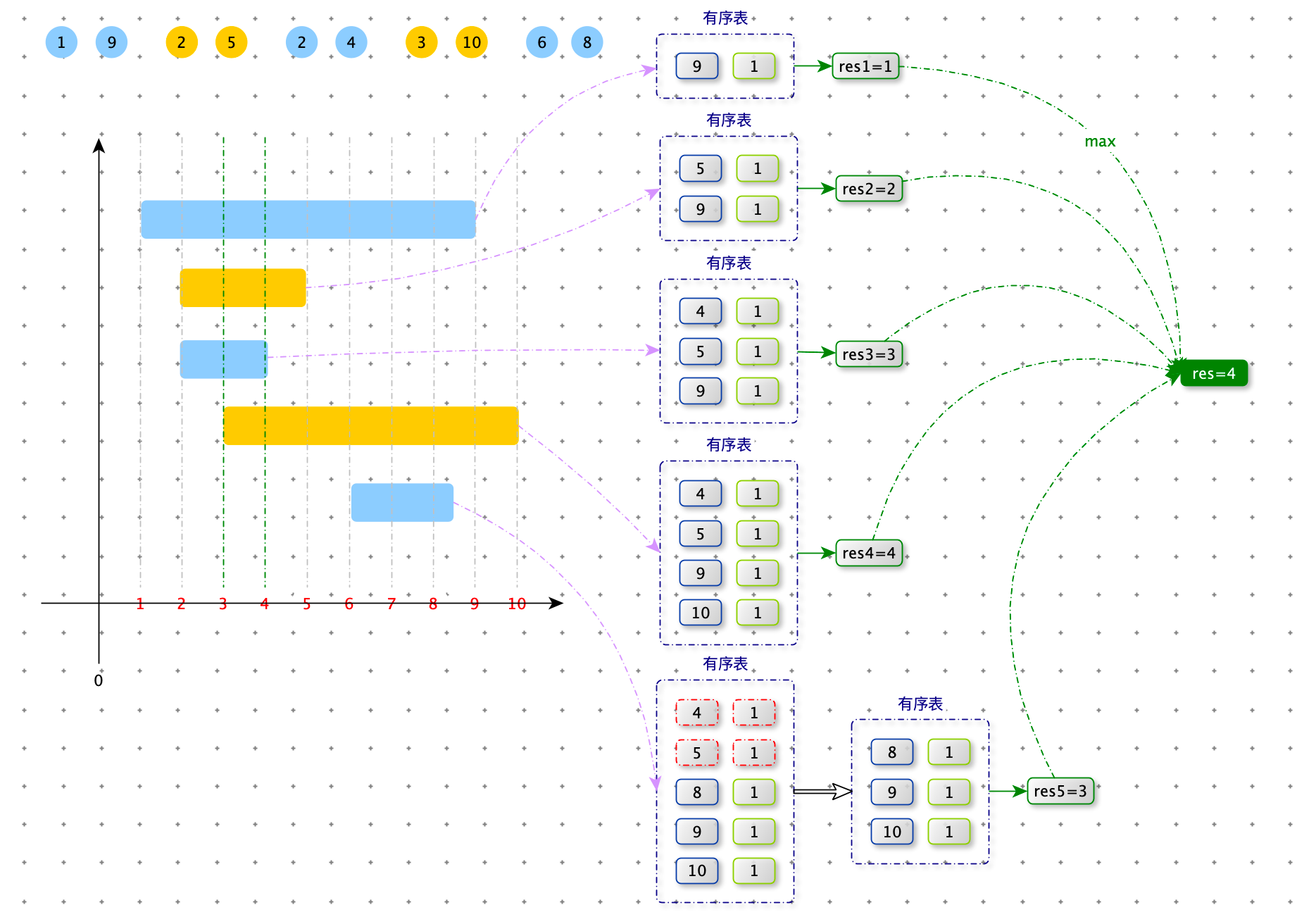
时间复杂度:$O(NlogN)$
空间复杂度:$O(N)$
public static int segmentCoverMax(int[][] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
// 排序
Arrays.sort(arr, (e1, e2) -> (e1[0] - e2[0]));
int res = 0;
// map 中 value 的和
int sum = 0;
// key:是 arr 的 end;value:end 的出现次数
TreeMap<Integer, Integer> map = new TreeMap<>();
for (int i = 0; i < arr.length; i++) {
int start = arr[i][0];
int end = arr[i][1];
int count = map.getOrDefault(end, 0) + 1;
map.put(end, count);
// map 中 value 的和增加了 1
sum += 1;
// 将 map 中所有 key( end ) 小于等于 start 的删除掉
while (true) {
Map.Entry<Integer, Integer> entry = map.floorEntry(start);
if (entry == null) {
break;
}
map.remove(entry.getKey());
// map 中 value 的和减少 entry.getValue()
sum -= entry.getValue();
start = entry.getKey();
}
res = Math.max(res, sum);
}
return res;
}
