给定一个正数 1,裂开的方法有一种:(1)
给定一个正数 2,裂开的方法有一种:(1,1),(2)
给定一个正数 3,裂开的方法有一种:(1,1,1),(1,2),(3)
给定一个正数 4,裂开的方法有一种:(1,1,1,1),(1,1,2),(1,3),(2,2),(4)
给定一个正数 n,求裂开的方法数。
亮点:斜率优化
方案一:暴力递归
f ( pre, rest )
- pre 只之前裂开的数
- rest 是本次要裂开的数。rest 要大于 pre。
- 返回结果:裂开的方法数
最终结果:f(1, n)
可能性分析:
从左向右的尝试模型。
f(i,j) 依赖:f(i+1, rest - (i+1))+ …+ f(n, n)
def ways(n):
return f(1, n)
def f(pre, rest):
if rest == 0: return 1
if rest < pre: return 0
res = 0
for i in range(pre, rest + 1):
res += f(i, rest - i)
return res
方案二:动态规划
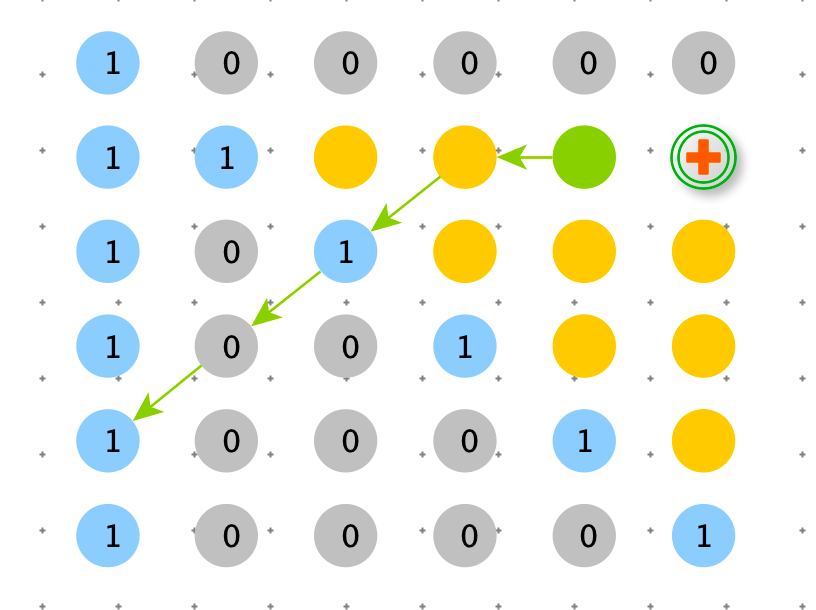
def ways1(n):
dp = [[0] * (n + 1) for _ in range(n + 1)]
for i in range(n + 1):
dp[i][0] = 1
dp[i][i] = 1
for pre in range(n - 1, 0, -1):
for rest in range(pre + 1, n + 1):
res = 0
for i in range(pre, rest + 1):
res += dp[i][rest - i]
dp[pre][rest] = res
return dp[1][-1]
方案三:动态规划–斜率优化
**斜率优化:看看邻近的解能否替换枚举行为。**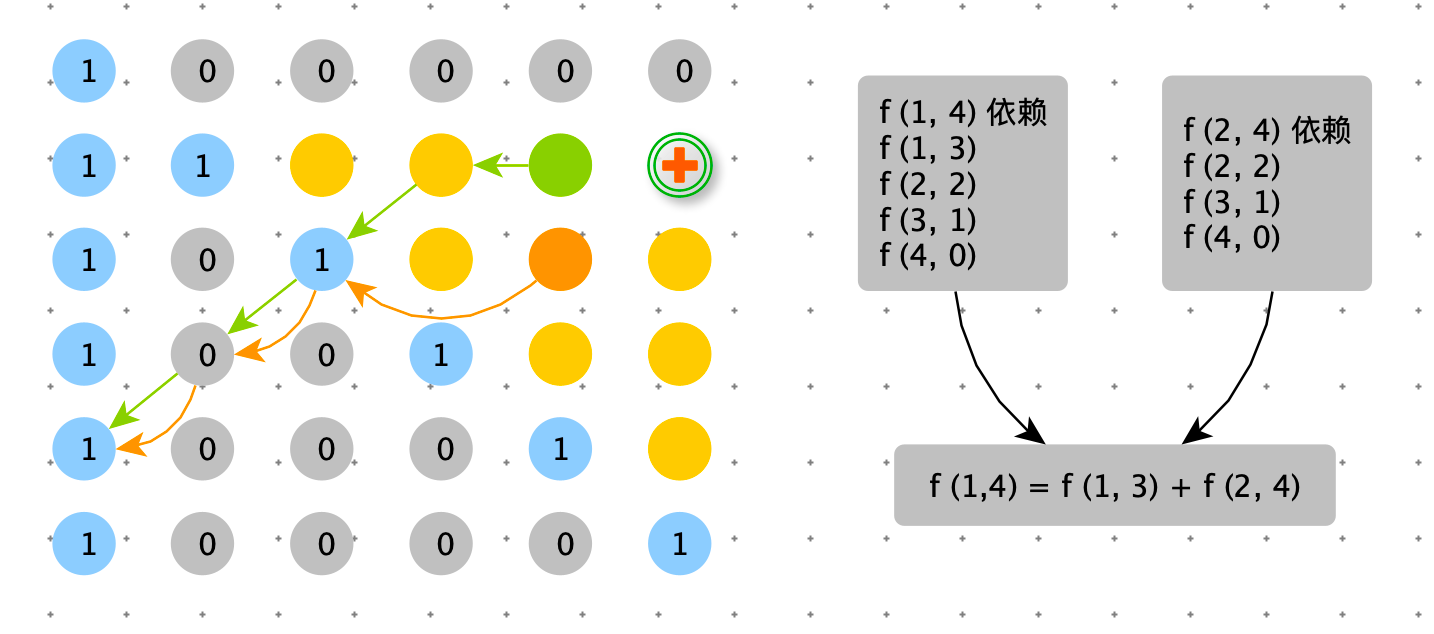
def ways2(n):
dp = [[0] * (n + 1) for _ in range(n + 1)]
for i in range(n + 1):
dp[i][0] = 1
dp[i][i] = 1
for pre in range(n - 1, 0, -1):
for rest in range(pre + 1, n + 1):
dp[pre][rest] = dp[pre][rest - pre] + dp[pre + 1][rest]
return dp[1][-1]
