给定一个二维数组 matrix,每个单元都是一个整数,有正有负。最开始的时候小 Q 操纵一条长度为 0 的蛇。蛇从矩阵最左侧人选一个单元格进入地图,蛇每次只能够到大当前位置的右上相邻,右侧相邻和右下相邻的单元格。蛇蛇到达一个单元格后,自身的长度会瞬间加上改单元格的数值,任何情况下长度为负则游戏结束。小 Q 是个天才,他拥有一个超能力,可以在游戏开始的时候把地图中的某一个节点的值变为相反数(注意:最多只能改变一个节点)。问小 Q 游戏过程中,他的蛇蛇最长长度可以到多少?
【例如】matrix =[ [ 1, -4, 10 ],
[ 3, -2, -1 ],
[ 2, -1, 0 ],
[ 0, 5, -2 ]]
最优路径为从最左侧的 3 开始, 3 -> -4 ( 利用能力变为 4 ) -> 10。所以返回 17
暴力递归
class Info:
def __init__(self, yes, no):
self.yes = yes
self.no = no
import sys
def snake(matrix):
res = - sys.maxsize
for row in range(len(matrix)):
for col in range(len(matrix[0])):
cur = process(matrix, row, col)
res = max(res, max(cur.yes, cur.no))
return res
def process(matrix, row, col):
if col == 0:
return Info(-matrix[row][0], matrix[row][0])
left = process(matrix, row, col - 1)
# 之前旅程中,一次能力也沒有用,能达到的最大路径和
pre_no = left.no if left.no >= 0 else -1
# 之前旅程中,用过一次能力,能达到的最大路径和
pre_yes = left.yes if left.yes >= 0 else -1
if row - 1 >= 0:
left_up = process(matrix, row - 1, col - 1)
# 如果为负数,说明已经死亡,这条尝试路径断了
if left_up.yes >= 0:
pre_yes = max(pre_yes, left_up.yes)
if left_up.no >= 0:
pre_no = max(pre_no, left_up.no)
if row + 1 < len(matrix):
left_down = process(matrix, row + 1, col - 1)
if left_down.yes >= 0:
pre_yes = max(pre_yes, left_down.yes)
if left_down.no >= 0:
pre_no = max(pre_no, left_down.no)
yes = no = -1
# 之前旅程中,no 这条尝试路径没有断
if pre_no >= 0:
# 当前 yes,之前旅途中 no + (当前翻转)
yes = pre_no - matrix[row][col]
# 当前 yes,之前旅途中 no + 不翻转
no = pre_no + matrix[row][col]
if pre_yes >= 0:
# 当前 yes,之前旅途中 no + (当前翻转)PK 之前旅途中 yes + 当前不翻转
yes = max(yes, pre_yes + matrix[row][col])
return Info(yes, no)
动态规划
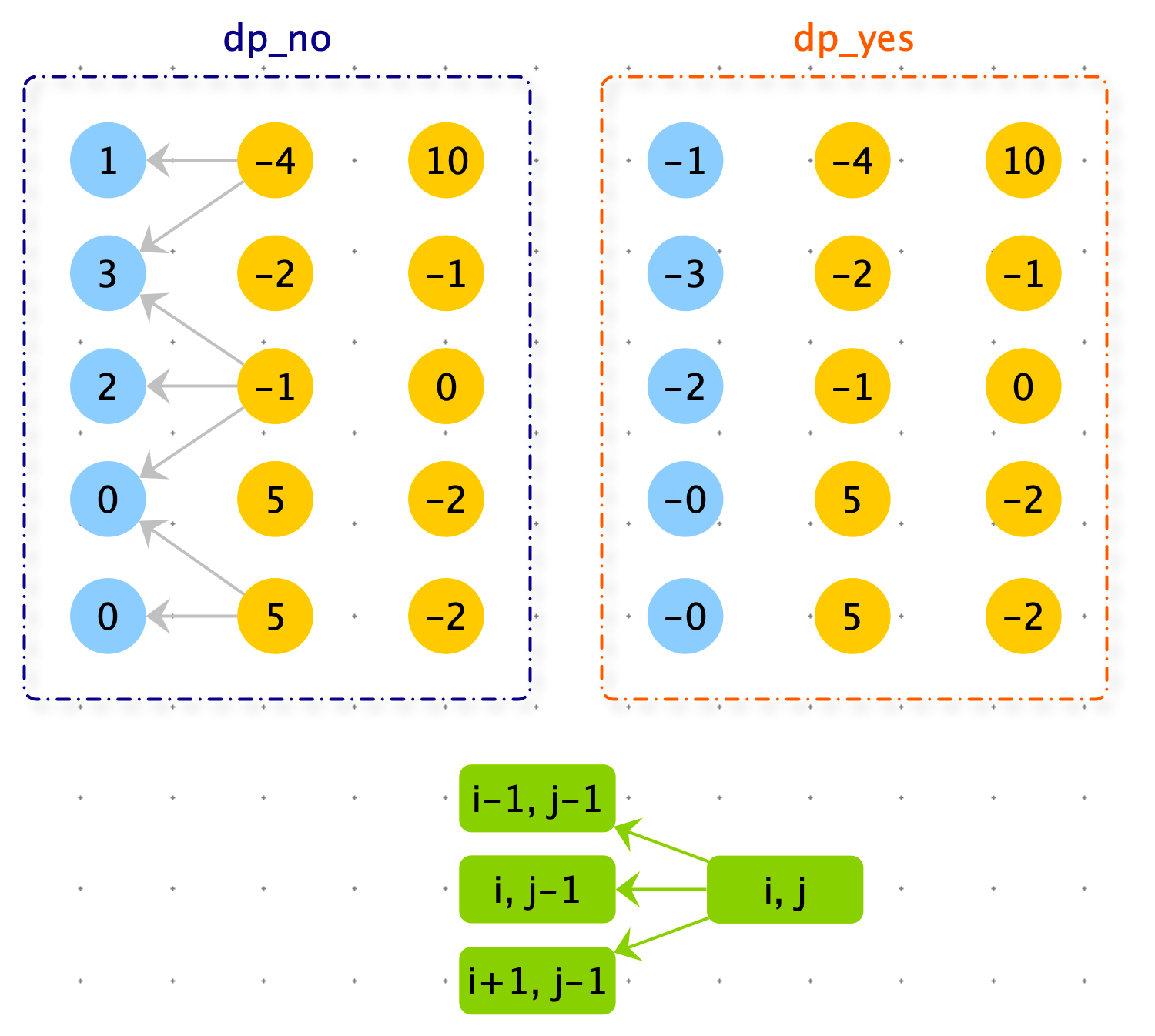
def snake3(matrix):
res = - sys.maxsize
dp_yes = [[-1] * len(matrix[0]) for _ in range(len(matrix))]
dp_no = [[-1] * len(matrix[0]) for _ in range(len(matrix))]
# base_case
for i in range(len(matrix)):
dp_yes[i][0] = -matrix[i][0]
dp_no[i][0] = matrix[i][0]
for col in range(1, len(matrix[0])):
for row in range(len(matrix)):
# 之前旅程中,一次能力也沒有用,能达到的最大路径和
pre_no = dp_no[row][col - 1] if dp_no[row][col - 1] >= 0 else -1
# 之前旅程中,用过一次能力,能达到的最大路径和
pre_yes = dp_yes[row][col - 1] if dp_yes[row][col - 1] >= 0 else -1
if row - 1 >= 0:
# 如果为负数,说明已经死亡,这条尝试路径断了
if dp_yes[row - 1][col - 1] >= 0:
pre_yes = max(pre_yes, dp_yes[row - 1][col - 1])
if dp_no[row - 1][col - 1] >= 0:
pre_no = max(pre_no, dp_no[row - 1][col - 1])
if row + 1 < len(matrix):
if dp_yes[row + 1][col - 1] >= 0:
pre_yes = max(pre_yes, dp_yes[row + 1][col - 1])
if dp_no[row + 1][col - 1] >= 0:
pre_no = max(pre_no, dp_no[row + 1][col - 1])
yes = no = -1
# 之前旅程中,no 这条尝试路径没有断
if pre_no >= 0:
# 当前 yes,之前旅途中 no + (当前翻转)
yes = pre_no - matrix[row][col]
# 当前 yes,之前旅途中 no + 不翻转
no = pre_no + matrix[row][col]
if pre_yes >= 0:
# 当前 yes,之前旅途中 no + (当前翻转)PK 之前旅途中 yes + 当前不翻转
yes = max(yes, pre_yes + matrix[row][col])
dp_yes[row][col] = yes
dp_no[row][col] = no
for row in range(len(matrix)):
for col in range(len(matrix[0])):
res = max(res, max(dp_no[row][col], dp_yes[row][col]))
return res
