给定一棵二叉树的头节点 head,已知所有节点的值都不一样,返回其中最大的且符合搜索二叉树的最大拓扑结构的大小。
拓扑结构:不是子树,只要能连起来的结构都算。
分析:
假设数组下标从 1 开始,我们可以根据数据的原始下标,通过公式推导出调整后的下标。
$f(i)=\begin{cases} 2i & i <=N & 左半区 \ 2(i-N)-1 & i>N & 右半区 \end{cases}$
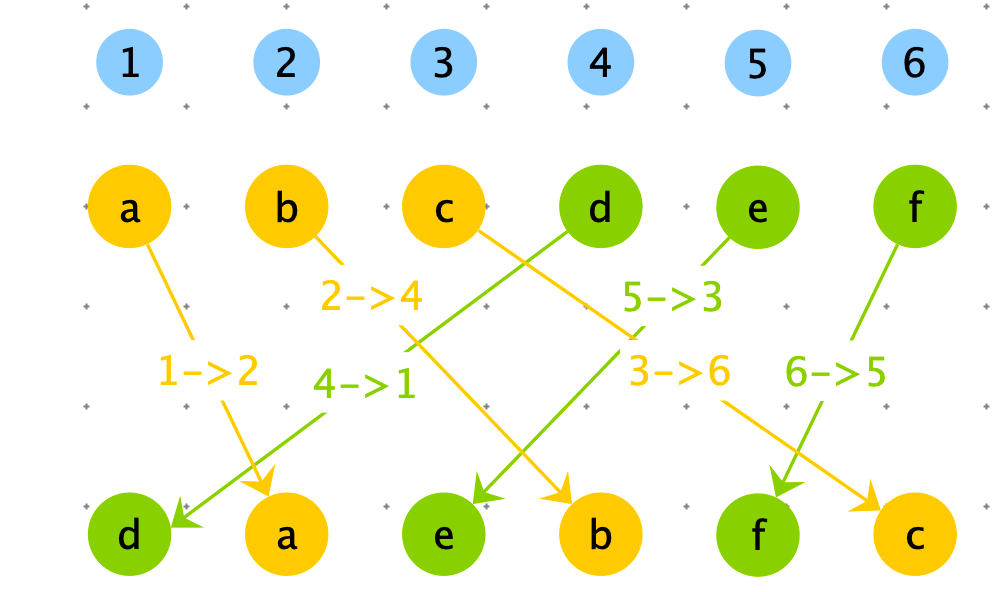
def modify_index(i, length):
if i <= int(length / 2): return 2 * i
return 2 * (i - int(length / 2)) - 1
def modify_index2(i, length):
return (2 * i) % (length + 1)
如果我们找到一个数据开始,如下图一样可以循环处理下去,就能完成调整。
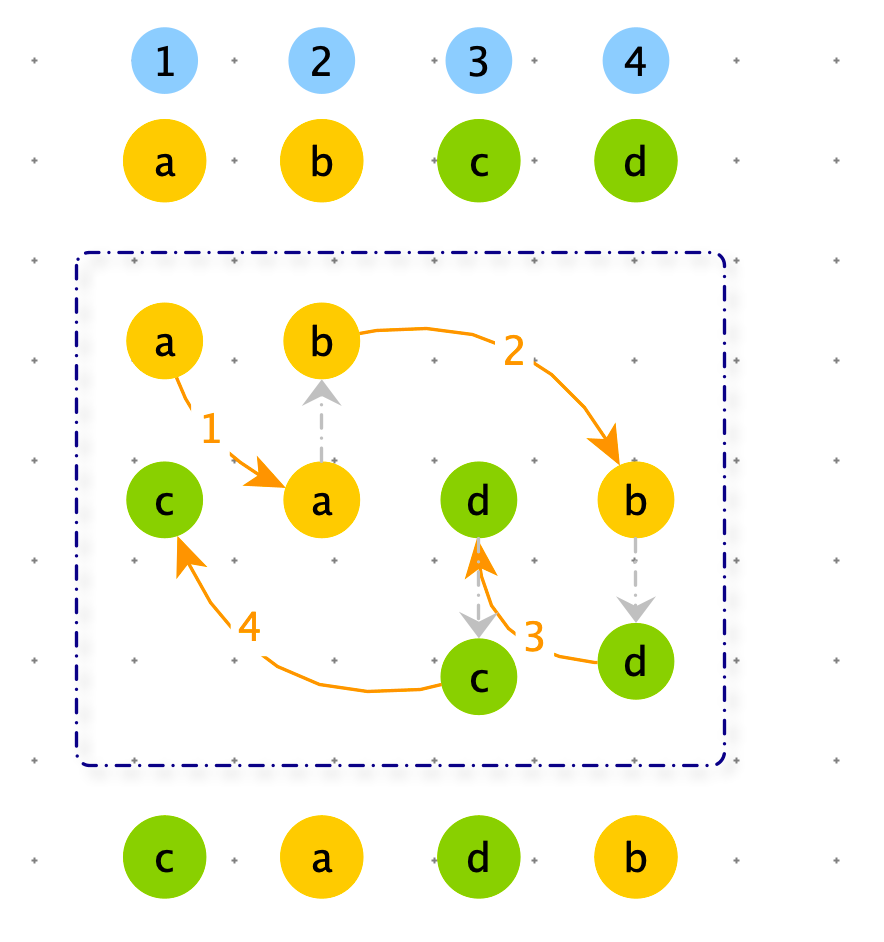
一个数组可能由很多环,我们需要处理完毕所有环。如果能找到所有环的触发点,问题就迎刃而解了。
下图的两个环,触发点分别是:a 和 c
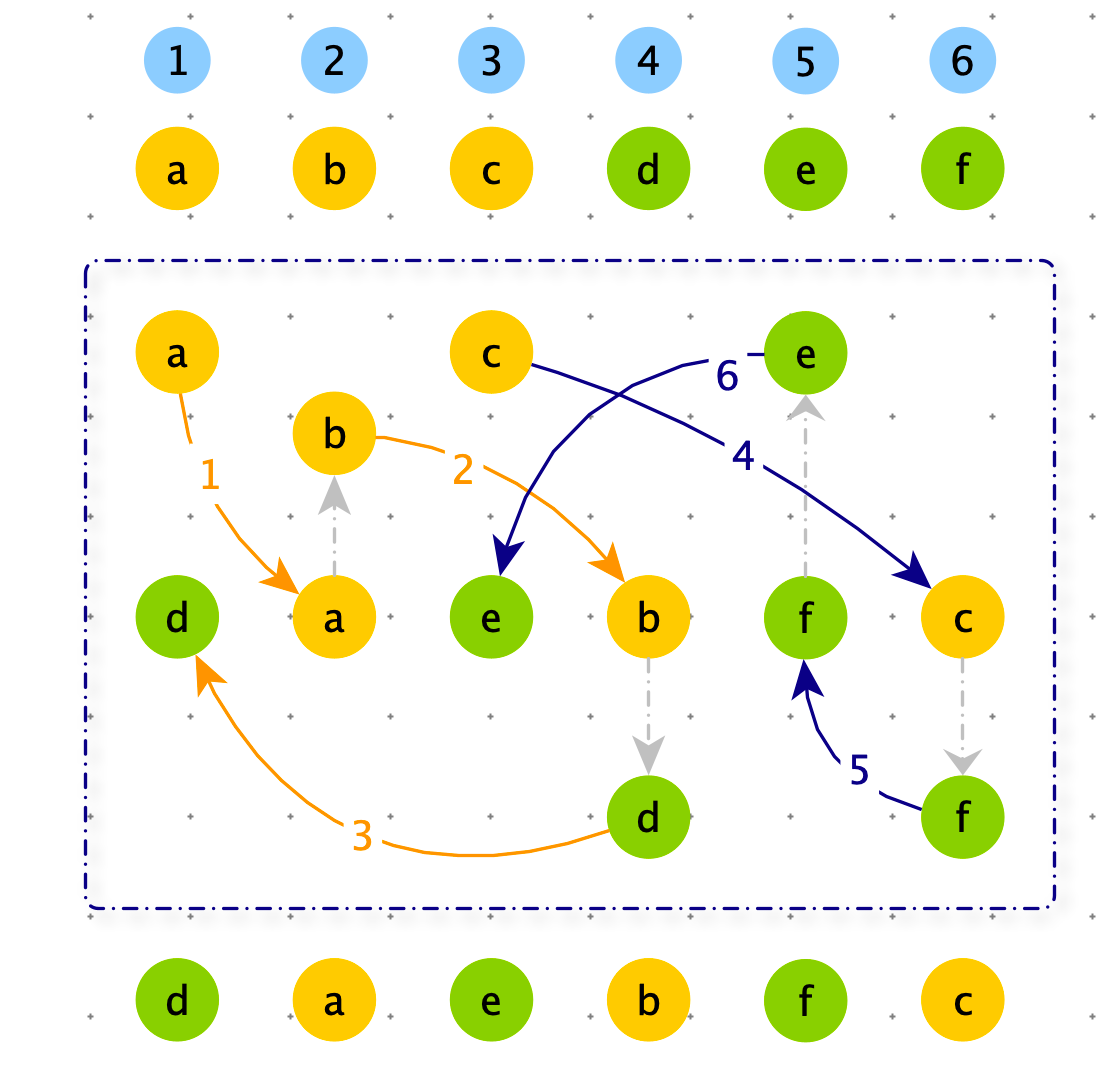
例如:
- 当 N = 2 时,触发点:1
- 当 N = 8 时,触发点:1,3
- 当 N = 26 时,触发点:1,3,9
对于arr 的长度为: $N=3^k-1$ ,通过以上方法解决了。
# 从 start 位置开始,向右 length 长度这一段,做下标续连推
# 出发位置(trigger):1,,3,9...
def cycles(arr, start,length, k):
# 找到每一个出发位置 trigger,一共 k 个
# 每个 trigger 都进行下标连续推
# 出发位置是从 1 开始计算的,而数组下标是 0 开始计算的
i = 0
trigger = 1
while i < k:
pre_value = arr[trigger + start - 1]
cur = modify_index2(trigger, length)
while cur != trigger:
tmp = arr[cur + start - 1]
arr[cur + start - 1] = pre_value
pre_value = tmp
cur = modify_index2(cur, length)
arr[cur + start - 1] = pre_value
trigger *= 3
i += 1
arr 的 长度为普通长度怎么办?
要处理普通长度数组的调整,我们需要先了解一种调整结构。
将数组【a,b,c,d,e,甲,乙】调整为 【甲,乙,a,b,c,d,e】步骤如下图。
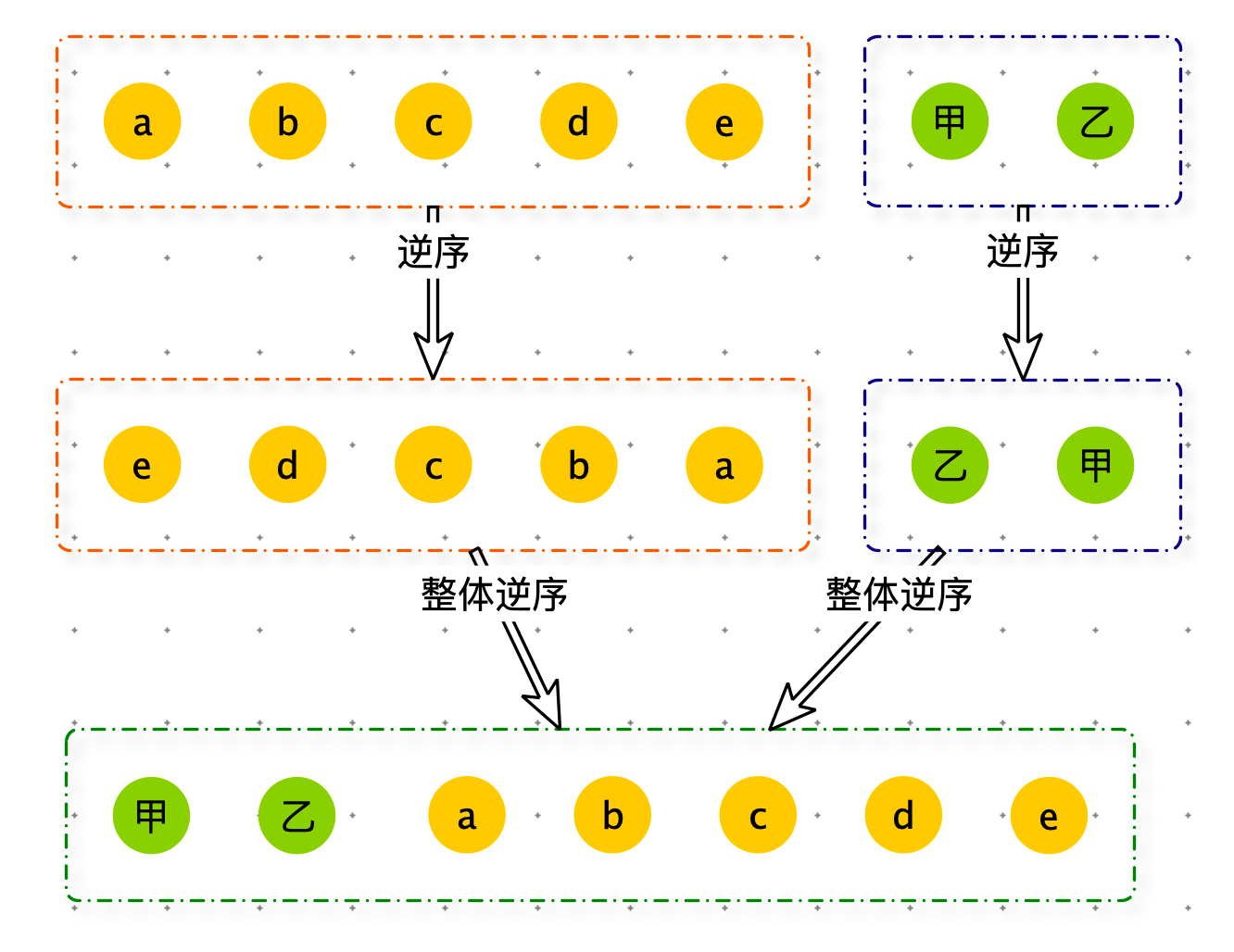
# arr[left:mid+1] 为左部分,arr[mid+1:right+1] 为右部分,左右部分互换
def rotate(arr, left, mid, right):
reverse(arr, left, mid)
reverse(arr, mid + 1, right)
reverse(arr, left, right)
def reverse(arr, left, right):
while left < right:
arr[left], arr[right] = arr[right], arr[left]
left += 1
right -= 1
开始处理通常偶数
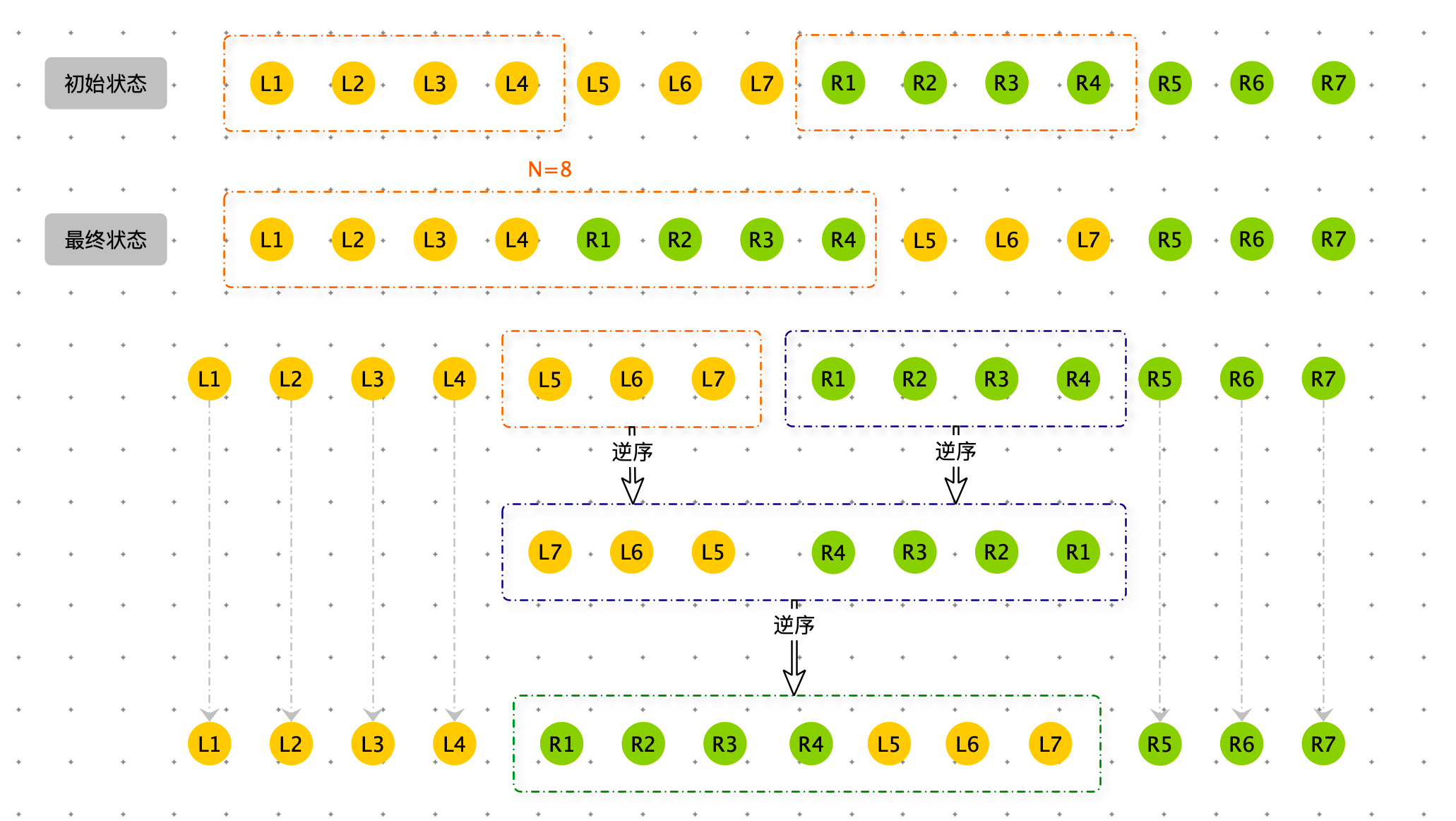
假设 N = 14, 距离 \(N=3^k-1\) 的数是 8,那么我们先处理前八位。我们需要将【L1,L2,L3,L4】和 【R1,R2,R3,R4】挨着。也就是:
原始数组:【L1,L2,L3,L4,L5,L6,L7,R1,R2,R3,R4,R5,R6,R7】
调整为: 【L1,L2,L3,L4,R1,R2,R3,R4,L5,L6,L7,R5,R6,R7】
此时我们按照: $N=3^k-1=8$ 处理, 当 N = 8 时,触发点:1,3。
处理完毕前8位,再处理剩余后六位:【L5,L6,L7,R5,R6,R7】
N = 6 距离 \(N=3^k-1\) 的数是 2,依次递归处理完毕。
def shuffle(arr):
if not arr or len(arr) % 2 != 0: return
proces(arr, 0, len(arr) - 1)
# 在 arr[left:right+1] 上做完美洗牌的调整
def proces(arr, left, right):
# 切成一块一块的解决,每一块的长度满足 3^k-1
while right > left - 1:
length = right - left + 1
base = 3
k = 1
# 计算小于等于 length 并且离 length 最近的,满足 3^k-1 的数
# 也就是找到最大的 k,满足 3^k <= length
while base <= int((length + 1) / 3):
base *= 3
k += 1
# 当前要解决长度为 base - 1 的块,一半就是再除2
half = int((base - 1) / 2)
# left 和 right 的中点位置
mid = int((left + right) / 2)
# 要旋转的左部分为[L + half...mid], 右部分为arr[mid + 1..mid + half]
# 注意在这里,arr下标是从 0 开始的
rotate(arr, left + half, mid, mid + half)
# 旋转完成后,从L开始算起,长度为base-1的部分进行下标连续推
cycles(arr, left, base - 1, k)
# 解决了前base - 1 的部分,剩下的部分继续处理
left = left + base - 1
对数器
import random
def wiggle_sort2(arr):
if not arr: return
# 假设这里是堆排序
arr.sort()
if len(arr) & 1 == 1:
proces(arr, 1, len(arr) - 1)
shuffle(arr)
for i in range(0, len(arr), 2):
tmp = arr[i]
arr[i] = arr[i + 1]
arr[i + 1] = tmp
def check():
for i in range(100):
arr = [int(random.random() * 100) for _ in range(int(random.random() * 10) + 1)]
arr1 = arr[:]
arr2 = arr[:]
shuffle(arr1)
shuffle2(arr2)
if arr1 != arr2:
print("ERROR", arr, arr1, arr2)
print("OVER")
wiggle sort
给出一个无序的数组,在原地将数组排列成符合以下规律:nums[0] <= nums[1] >= nums[2] <= nums[3]….
Given nums = [3, 5, 2, 1, 6, 4], one possible answer is [1, 6, 2, 5, 3, 4].
空间复杂度要求:O(1)
第一步先排序:
使用堆排序(三大排序算法:快排,堆排序,归并排序中只有堆排序的空间复杂度为:O(1))
第二步:
如果 N 是偶数:进行完美洗牌,完美洗牌后大数在第一位,需要将相邻两数两两交换顺序。
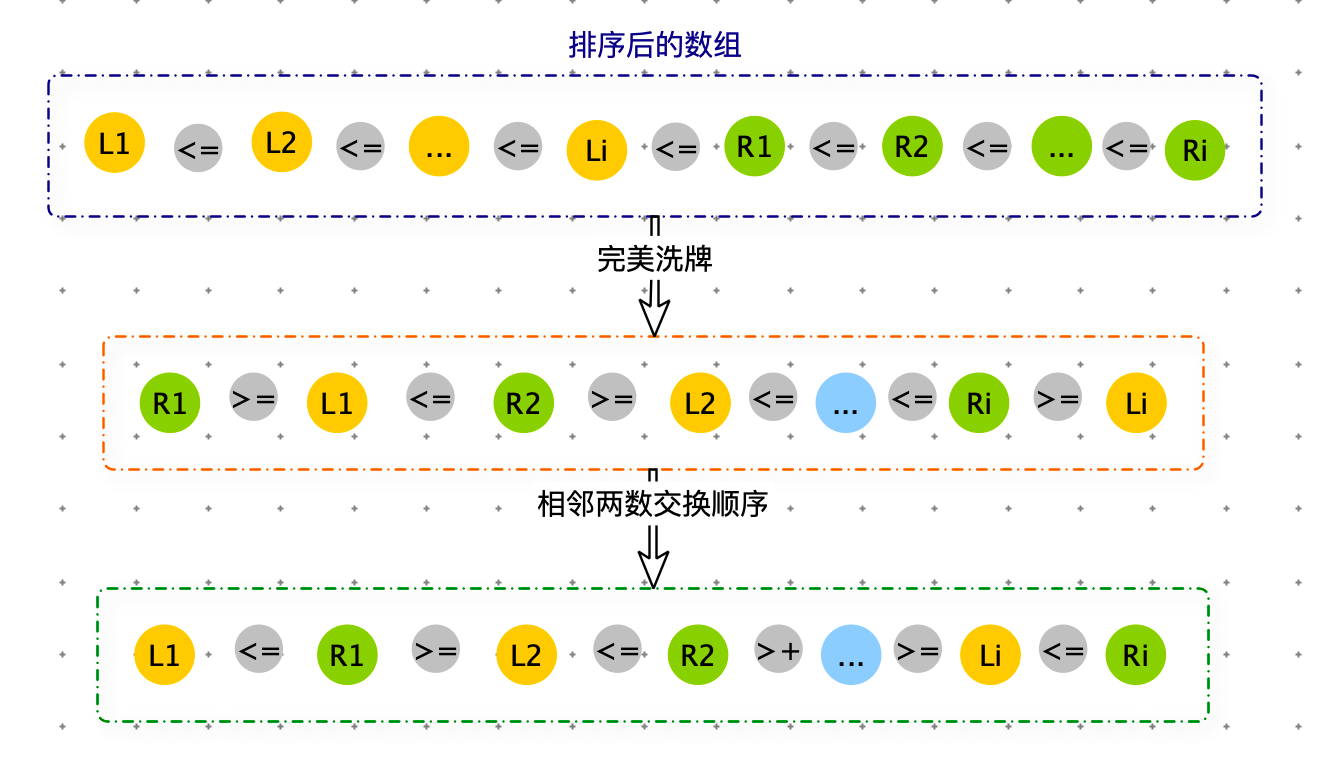
如果 N 是奇数:对arr[1:] 进行完美洗牌。
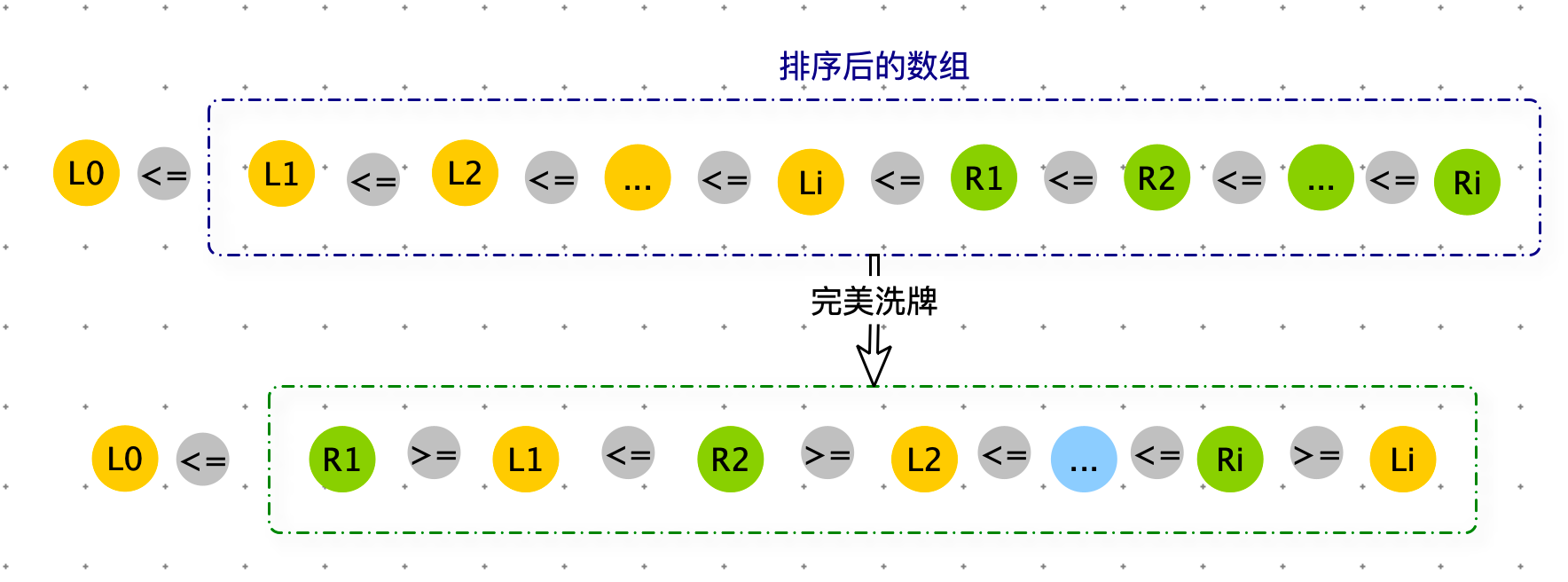
def wiggle_sort(arr):
if not arr: return
# 假设这里是堆排序
arr.sort()
if len(arr) % 2 == 0:
return shuffle(arr)
return proces(arr, 1, len(arr) - 1)
