给定两个字符串 str1 和 str2 ,求两个字符串的最长公共子序列。
方案一:暴力递归
可能性分析
f( i, j ) 定义:string1[:i] 和 string2[:j] 两个子串的最长公共子序列的长度。注意:此时或者的最长公共子序列不要求必须以 string1[i] 和 string[2] 结尾。
$f(i,j)=\begin{cases} f(i-1,j-1)+1 & string1[i]==string2[j] \ max(f(i-1,j),f(i,j-1)) & string1[i]!=string2[j] \end{cases}$
basecase
- i < 0 or j < 0 没有公共子序列返回 0
- i = 0 and j !=0 ,在 string2[:j] 如果出现过 string1[0] 最长公共子序列长度为 1,否则为 0
- j = 0 and i !=0 ,在 string1[:i] 如果出现过 string2[0] 最长公共子序列长度为 1,否则为 0
最终结果
f( len(string1) - 1 , len(string2) - 1 ) 表示string1 和 string2 的最长公共子序列的长度,因此可以直接返回。
def longest_common_subsequence(string1, string2):
if not string1 or not string2: return 0
return f(string1, string2, len(string1) - 1, len(string2) - 1)
def f(string1, string2, i, j):
# base case
if i < 0 or j < 0: return 0
if i == 0 and j != 0:
for k in range(j + 1):
if string2[k] == string1[i]:
return 1
return 0
if i != 0 and j == 0:
for k in range(i + 1):
if string1[k] == string2[j]:
return 1
return 0
if string1[i] == string2[j]:
return f(string1, string2, i - 1, j - 1) + 1
return max(f(string1, string2, i, j - 1), f(string1, string2, i - 1, j))
方案二:动态规划
依赖分析
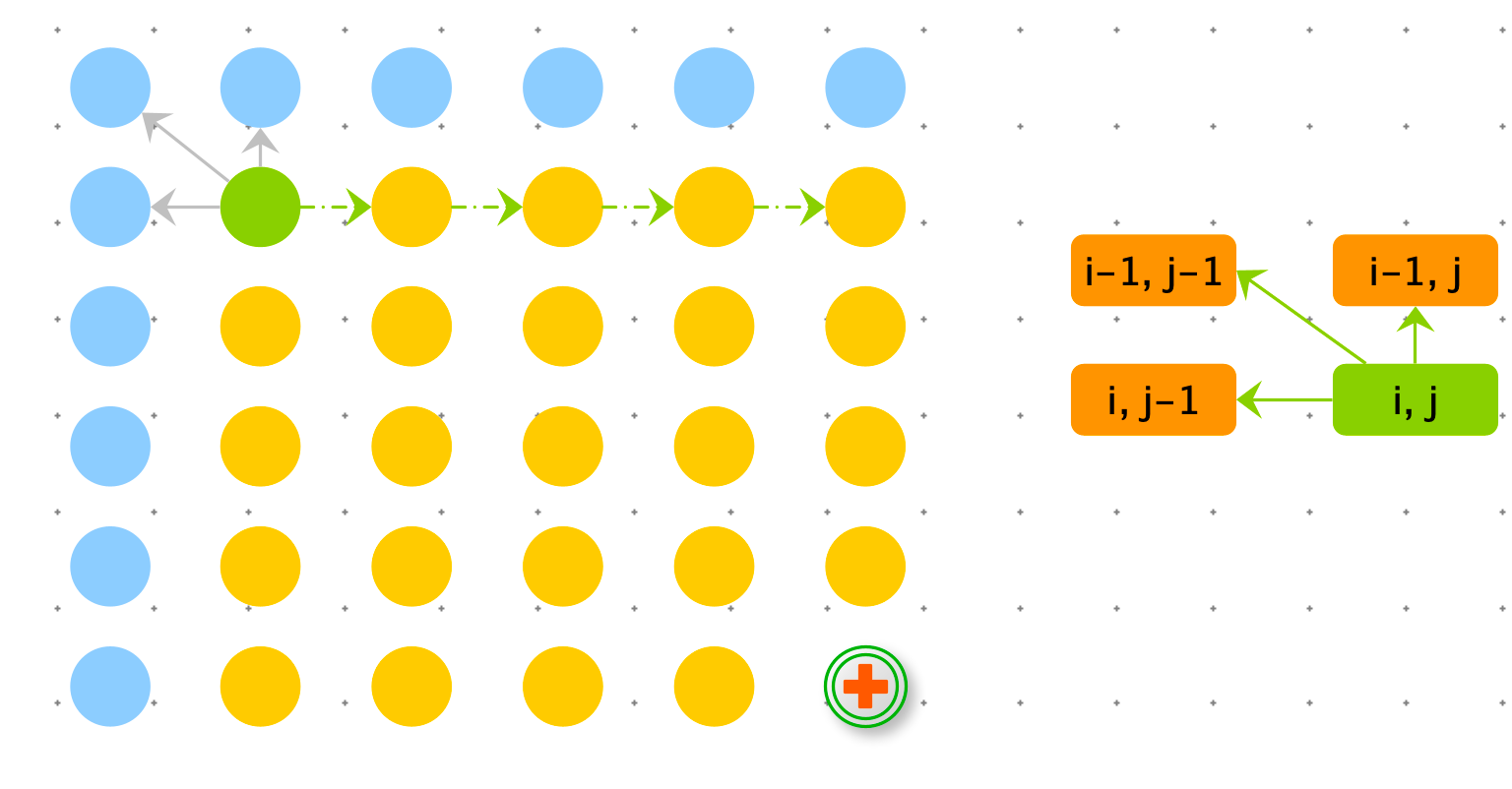
def longest_common_subsequence1(string1, string2):
if not string1 or not string2: return 0
dp = [[0] * len(string2) for _ in range(len(string1))]
# base case
dp[0][0] = 1 if string1[0] == string2[0] else 0
for i in range(1, len(string1)):
dp[i][0] = max(dp[i - 1][0], 1 if string1[i] == string2[0] else 0)
for i in range(1, len(string2)):
dp[0][i] = max(dp[0][i - 1], 1 if string1[0] == string2[i] else 0)
for row in range(1, len(string1)):
for col in range(1, len(string2)):
if string1[row] == string2[col]:
dp[row][col] = dp[row - 1][col - 1] + 1
else:
dp[row][col] = max(dp[row][col - 1], dp[row - 1][col])
return dp[-1][-1]
方案三:动态规划之滚动数组

def longest_common_subsequence2(string1, string2):
if not string1 or not string2: return 0
dp = [0] * len(string2)
# base case
dp[0] = 1 if string1[0] == string2[0] else 0
for i in range(1, len(string2)):
dp[i] = max(dp[i - 1], 1 if string1[0] == string2[i] else 0)
for row in range(1, len(string1)):
left_up = dp[0]
dp[0] = max(dp[0], 1 if string2[0] == string1[row] else 0)
for col in range(1, len(string2)):
if string1[row] == string2[col]:
new_value = left_up + 1
else:
new_value = max(dp[col - 1], dp[col])
left_up = dp[col]
dp[col] = new_value
return dp[-1]
上述三个方案只是求出最长公共子序列的长度。
方案一:暴力递归–最长公共子序列
class Info:
def __init__(self, length, res):
self.length = length
self.res = res
def longest_common_subsequence(string1, string2):
if not string1 or not string2: return ""
info = f(string1, string2, len(string1) - 1, len(string2) - 1)
return ''.join(info.res)
def f(string1, string2, i, j):
# base case
if i < 0 or j < 0: return Info(0, [])
if i == 0 and j != 0:
for k in range(j + 1):
if string2[k] == string1[i]:
return Info(1, [string2[k]])
return Info(0, [])
if i != 0 and j == 0:
for k in range(i + 1):
if string1[k] == string2[j]:
return Info(1, [string1[k]])
return Info(0, [])
if string1[i] == string2[j]:
info = f(string1, string2, i - 1, j - 1)
res = info.res[:]
res.append(string1[i])
return Info(info.length + 1, res)
info1 = f(string1, string2, i, j - 1)
info2 = f(string1, string2, i - 1, j)
length = info1.length
res = info1.res[:]
if info2.length > length:
length = info2.length
res = info2.res[:]
return Info(length, res)
方案二:动态递归–最长公共子序列
def longest_common_subsequence1(string1, string2):
if not string1 or not string2: return ""
dp = [[0] * len(string2) for _ in range(len(string1))]
# base case
dp[0][0] = 1 if string1[0] == string2[0] else 0
for i in range(1, len(string1)):
dp[i][0] = max(dp[i - 1][0], 1 if string1[i] == string2[0] else 0)
for i in range(1, len(string2)):
dp[0][i] = max(dp[0][i - 1], 1 if string1[0] == string2[i] else 0)
for row in range(1, len(string1)):
for col in range(1, len(string2)):
if string1[row] == string2[col]:
dp[row][col] = dp[row - 1][col - 1] + 1
else:
dp[row][col] = max(dp[row][col - 1], dp[row - 1][col])
# 根据 dp 反向求出最长公共子序列
row = len(string1) - 1
col = len(string2) - 1
# 最长公共子序列的长度
index = dp[-1][-1]
res = [None] * index
while index > 0:
# 如果dp[row][col] == dp[row - 1][col] 向上走一步
if row > 0 and dp[row][col] == dp[row - 1][col]:
row -= 1
# 如果 dp[row][col] == dp[row][col-1] 向左走一步
elif col > 0 and dp[row][col] == dp[row][col - 1]:
col -= 1
else:
# dp[row][col] - dp[row-1][col-1] ==1 and string1[row] == string2[col]
# 那么向左上走一步,并记录 string1[row] or string2[col]
index -= 1
res[index] = string1[row]
row -= 1
col -= 1
return ''.join(res)
