背景
搜索系统优化长尾 query。想了解一下长尾 query 长什么样?大体上都有几类?最好能归类,一类一类处理。
Query 数据源:包含“什么”,“怎么”,“如何” 关键词的 Query。

K-means
聚类概念
生活中的聚类例子:班级分组。
一个班级有 40 名学生,班主任分别让小明,小红,小强,小李将班级中学生分成两组。
小明:男生一组,女生一组。
小红:前三排一组,后三排一组。
小强:左三列一组,右三列一组。
小李:住校生一组,走读生一组。
为什么造成大家的分组不一样?是因为老师没有给明确定分组规则。
聚类是无监督学习。
无监督学习不需要标注数据。
有监督学习需要标注数据。NB,LR。
聚类:将数据划分到不同的类里,使相似(距离相近)的数据在同一类里,不相似(距离较远)的数据在不同的类里。
Demo
生成模拟数据
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# 生成:样本数500,特征数为2,4 个中心的样本集
X, y = make_blobs(n_samples=500, n_features=2, centers=4, random_state=1)
plt.scatter(X[:, 0], X[:, 1], marker='o', s=8)
plt.show()
X = [[-6.92324165e+00 -1.06695320e+01] [-8.63062033e+00 -7.13940564e+00] [-9.63048069e+00 -2.72044935e+00] [-2.30647659e+00 5.30797676e+00]]
模拟的数据的分布:

聚类及可视化代码(使用 sklearn 库中的 KMeans):
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
# 生成:样本数500,特征数为2,4 个中心的样本集
X, y = make_blobs(n_samples=500, n_features=2, centers=4, random_state=1)
# 聚类
n_clusters = 4
cluster = KMeans(n_clusters=n_clusters, random_state=0).fit(X)
# 可视化 -- 样本
color = ["red", "pink", "orange", "gray"]
y_pred = cluster.labels_
for i in range(n_clusters):
plt.scatter(X[y_pred == i, 0], X[y_pred == i, 1], marker='o', s=8, c=color[i])
# 可视化 -- 质心
centroid = cluster.cluster_centers_
plt.scatter(centroid[:,0], centroid[:,1], marker='x', s=15, c="black")
plt.show()
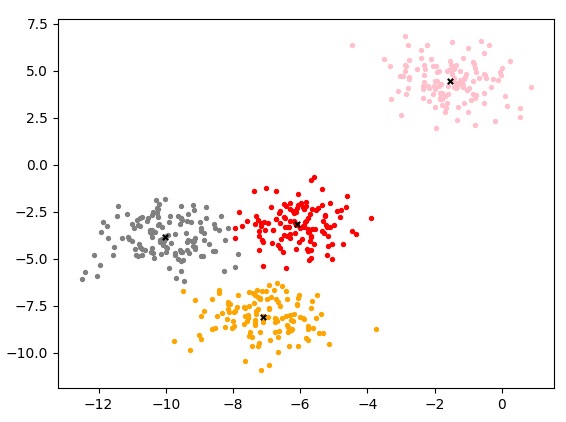
聚类的结果:不同颜色表示不同类型
欧式距离
点 X 到点 Y 的距离。
$dist(X,Y) = \sqrt{\sum_{i=1}^n{(x_i-y_i)^2}}$
如图:点 $P_1(x_1,y_1) $ 与点$P_2(x_2,y_2)$ 之间的距离为:$\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$

K-Means 算法
算法描述
算法描述
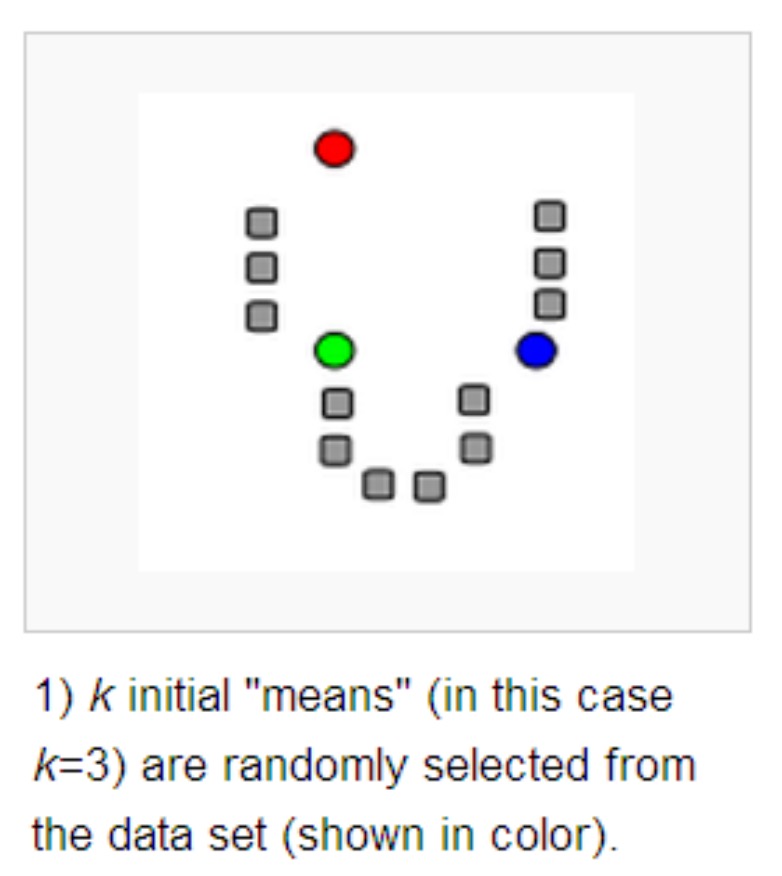
- 从数据集中随机选取 K 个样本,作为初始质心。
- 重新对样本划分类别:计算每个样本 $x_i$ ,计算它到每一个质心的距离,将其分配到距离最小质心所对应的类中。
- 重新计算每个质心。$c_i = \frac{1}{\vert c_i \vert }\sum_{x \in c_i}x$
- 当满足一定条件,如类别划分不在变化时或者达到最大迭代轮数,则终止算法,否则继续步骤 2 和 3。
$dist(x,y)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$
例如:绿色类中点:$A:[x_1,y_1] \,, B:[x_2,y_2]\,,C:[x_3,y_3]\,,D:[x_4,y_4]$
更新绿色质心:$[\frac{x_1+x_2+x_3+x_4}{4},\frac{y_1+y_2+y_3+y_4}{4}]$
**注意:此时的质心是虚拟的点(不是训练集中的样本,后续优化点)**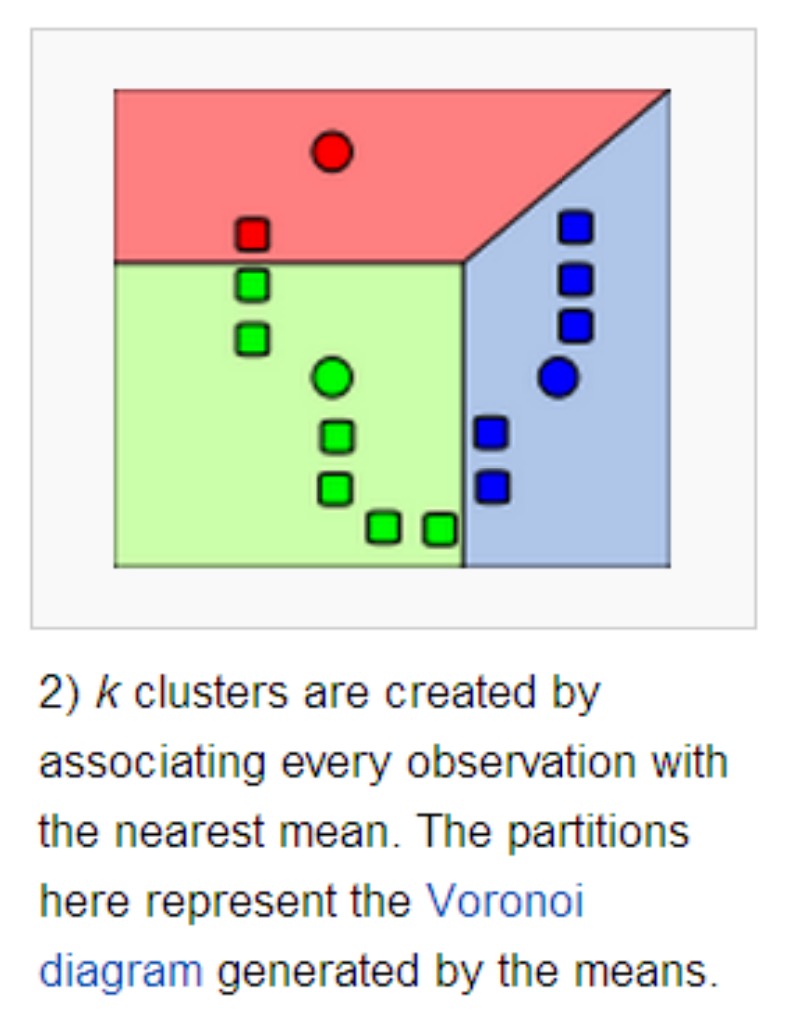
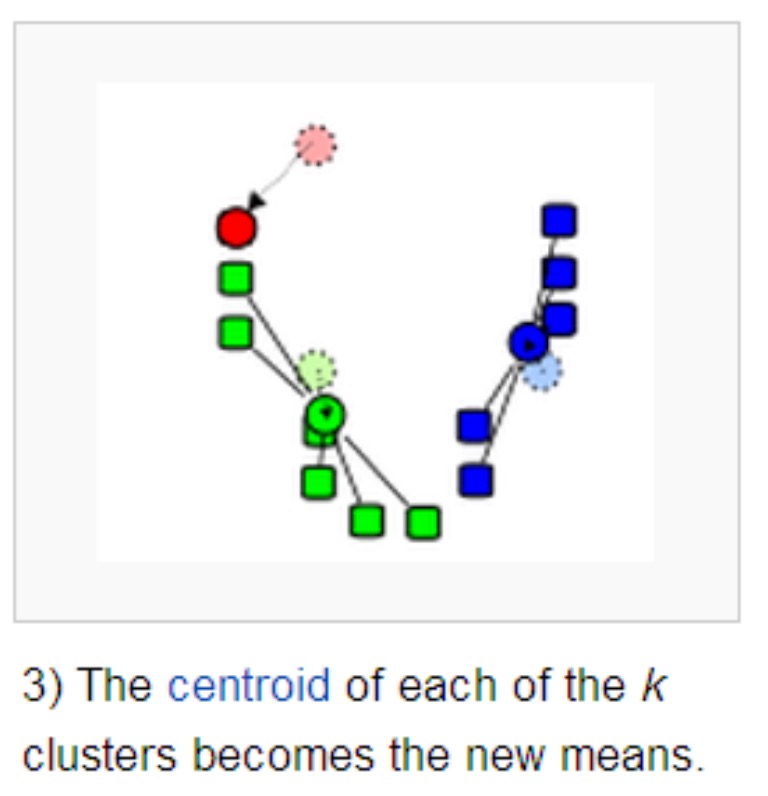

关键点:
-
计算样本数据与中心点的距离
欧式距离:$dist(X,Y) = \sqrt{\sum_{i=1}^n{(x_i-y_i)^2}}$
-
计算聚类的中心点(更新质心)
均值。
-
算法终止条件:最小化 WCSS
$L(C) = \sum_{k \in K}\sum_{i \in k}|x_i-c_k|^2$
Kmeans 聚类代码(自己实现方便后根据业务需求优化聚类过程):
import math
from random import sample
class Kmeans:
def __init__(self):
self.centorids = []
self.labels = []
# 训练
def train(self, train_data, n_clusters=10, max_iter=300):
last_wcss = 0.0
iter_count = 0
centorids = [train_data[i] for i in sample(range(len(train_data)), n_clusters)]
print("kmeans train start:", centorids)
while True:
labels = [[] for _ in range(n_clusters)]
wcss = 0
# 聚类
for x_id in range(len(train_data)):
min_distance = math.inf
for cluster_id in range(n_clusters):
distance = self.calc_distance(train_data[x_id], centorids[cluster_id])
if min_distance > distance:
min_distance = distance
cluster = cluster_id
labels[cluster].append(x_id)
wcss += min_distance
print("kmeans wcss:", wcss, iter_count)
# modify centers
for cluster_id in range(n_clusters):
centorids[cluster_id] = self.calc_centroid(train_data, labels[cluster_id])
iter_count += 1
if last_wcss == wcss or iter_count == max_iter: break
last_wcss = wcss
self.centorids = centorids
tmp = sorted([(x_id, cluster_id) for cluster_id in range(len(labels)) for x_id in labels[cluster_id]])
self.labels = [cluster_id for x_id, cluster_id in tmp]
print("kmeans train Over")
# 计算质心
def calc_centroid(self, train_data, cluster_data):
x_dimension = len(train_data[0])
centroid = [0.0] * x_dimension
for x_id in cluster_data:
for i in range(x_dimension):
centroid[i] += train_data[x_id][i]
return [item / len(cluster_data) for item in centroid]
# 计算距离
def calc_distance(self, x, y):
return math.sqrt(sum([math.pow(i - j, 2) for i, j in zip(x, y)]))
# 测试
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as np
# 生成:样本数500,特征数为2,4 个中心的样本集
X, y = make_blobs(n_samples=500, n_features=2, centers=4, random_state=1)
# 聚类
kmeans = Kmeans()
kmeans.train(X, k=4)
# 可视化
color = ["red", "pink", "orange", "gray"]
# 可视化 -- 样本
y_pred = np.array(kmeans.labels)
for i in range(n_clusters):
plt.scatter(X[y_pred == i, 0], X[y_pred == i, 1], marker='o', s=8, c=color[i])
# 可视化 -- 质心
centroid = np.array(kmeans.centorids)
plt.scatter(centroid[:, 0], centroid[:, 1], marker='x', s=15, c="black")
plt.show()
聚类的结果:不同颜色表示不同类型
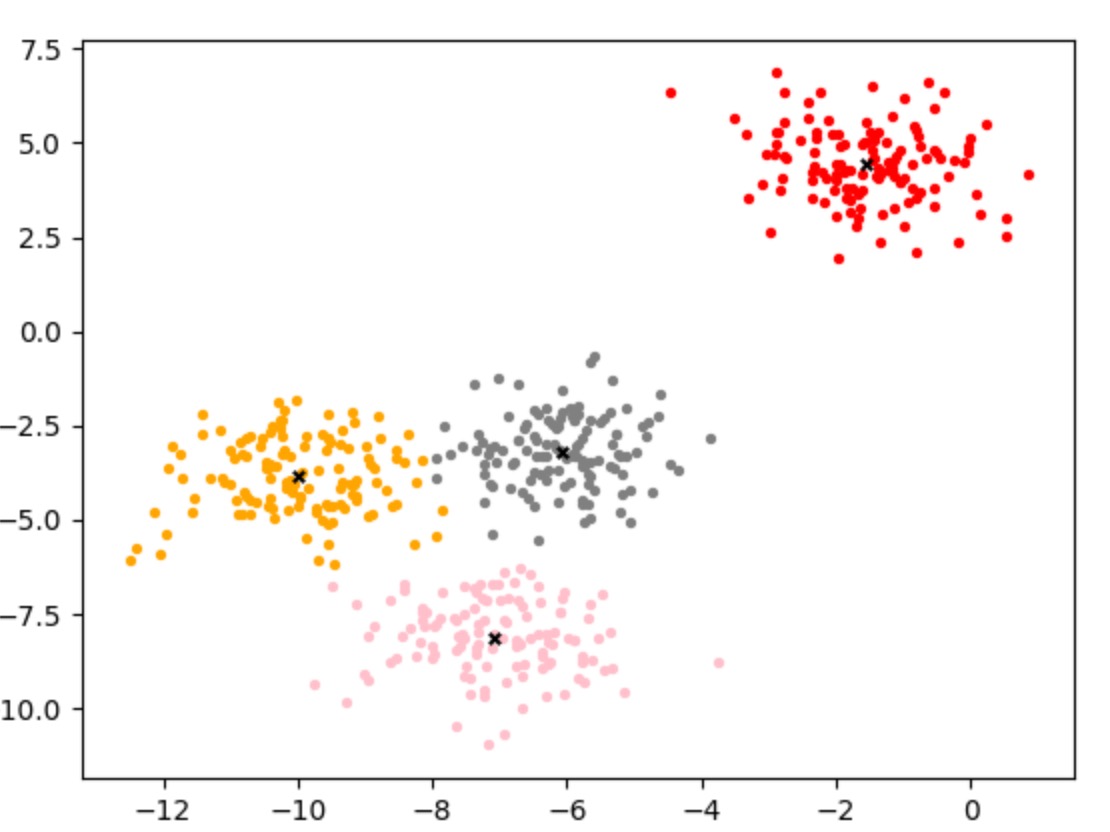
K-Means 缺点
- K 的选择需要事先预定:K值的选取不好把握。(改进:ISODATA 算法)
- K 个初始质心的位置选择对聚类结果和运行时间都有很大影响。(改进:k-means++)
- 采用迭代方法,得到的结果只是局部最优。
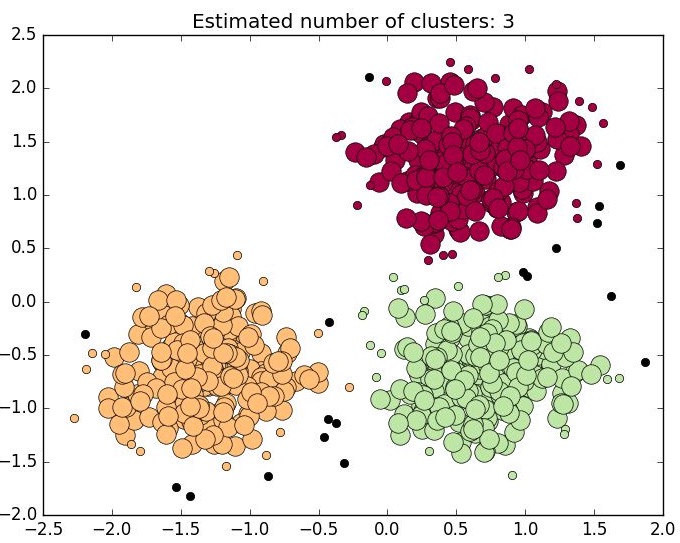
如下图:红色圆圈是初始质心的位置,由于初始质心的位置不同,最终聚类的结果也不同。


K-Means++
由于初始质心对分类结果及收敛速度影响甚大,所以K-Means ++ 对初始质心进行优化。
==核心思想:初始质心相互距离尽可能远。==

算法描述
- 步骤一:随机选取一个样本作为第一个聚类质心:$c_1$
- 步骤二:
- 计算每个样本与当前已有质心的最短距离(即与最近的一个质心的距离),用 D(x)表示。
- D(x) 越大,表示被选取作为质心的概率越大。概率公式:$\frac{D(x)^2}{\sum_{x \in X}{D(x)^2}}$
- 用轮盘法选出下一个质心。
- 步骤三:重复步骤二,直到选出 k 个质心。
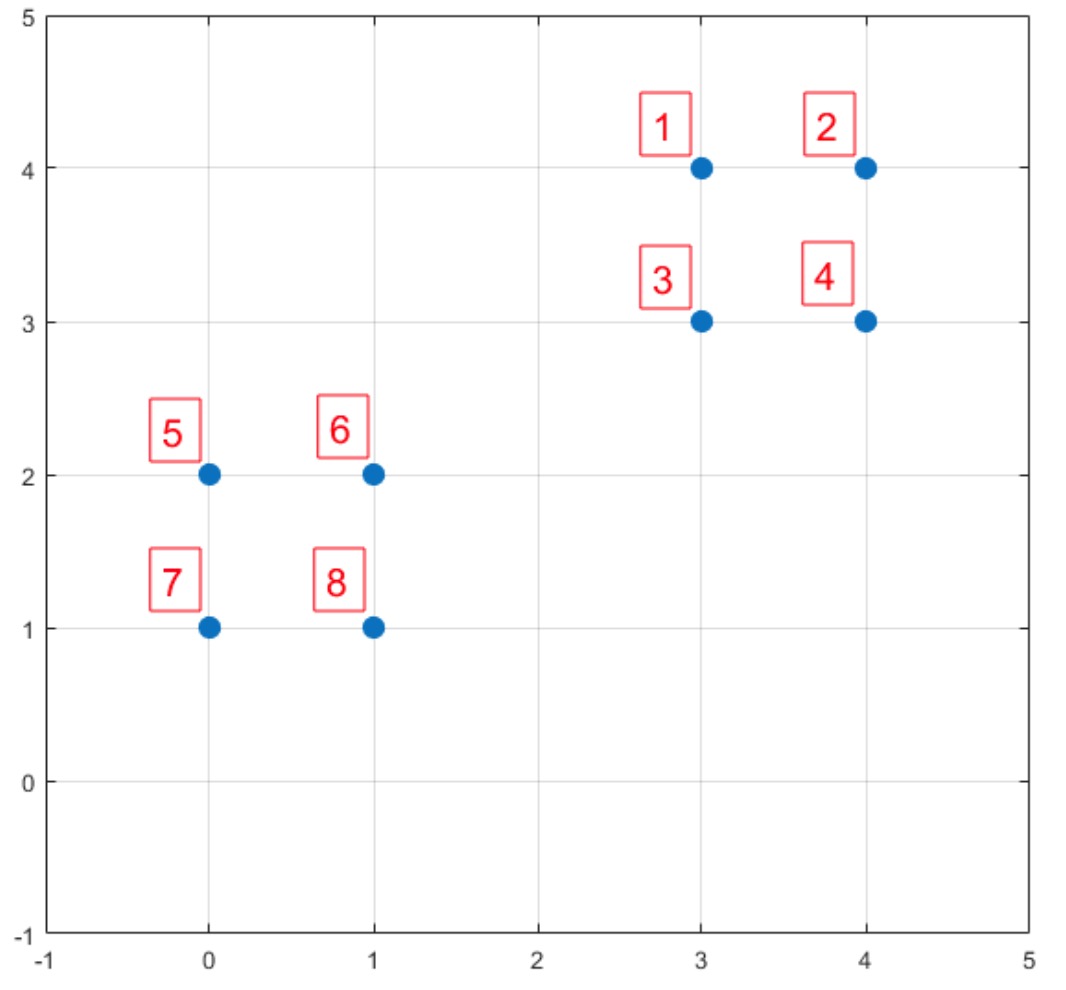
数据点:1:( 3 , 4 ),2:( 4 , 4 ),3:( 3 , 3 ),4:( 4 , 3 ),5:( 0 , 2 ),6:( 1 , 2 ),7:( 0 , 1 ),8:( 1 , 1 )
$dist(X,Y) = \sqrt{\sum_{i=1}^n{(x_i-y_i)^2}}$
步骤一:$c1 = $ 6 号点。
步骤二:
-
计算所有样本的 D(x)。
序号 1 2 3 4 5 6 7 8 D(x) $2\sqrt2$ $\sqrt{13}$ $\sqrt5$ $\sqrt{10}$ 1 0 $ \sqrt2 $ 1 $D(x)^2$ 8 13 5 10 1 0 2 1 P(x) 0.2 0.325 0.125 0.25 0.025 0 0.05 0.025 Sum 0.2 0.525 0.65 0.9 0.925 0.925 0.975 1 P(x) 就是每个样本被选为下一个质心的概率。
sum 是概率 P(x) 的累加,用于轮盘法。

节点1,2,3,4 的被选中的概率是90%。从图上看,这四个节点,选为下一个质心更好。
这样验证了:K-Means++ 的思想:核心思想:初始质心相互距离尽可能远。
Sum(D(x)) * random.random()
def get_closest_dist(self, point, centroids):
min_dist = math.inf
for i, centroid in enumerate(centroids):
dist = self.calc_distance(centroid, point)
if dist < min_dist:
min_dist = dist
return min_dist
def kpp_centers(self, train_data, k):
centroids = [random.choice(train_data)]
d = [0.0] * len(train_data)
for _ in range(1, k):
total = 0.0
for i, point in enumerate(train_data):
d[i] = self.get_closest_dist(point, centroids)
total += d[i]
total *= random.random()
for i, di in enumerate(d):
total -= di
if total > 0: continue
centroids.append(train_data[i])
break
return centroids
ISODATA 算法
K-Means 和 K-Means++ 质心个数 K 是固定不变的。ISODATA 算法通过:==分裂和合并==,来调整质心个数。
ISODATA 算法的超参数
- 预期质心个数:$K_0$,算法的质心数的变动范围由 $K_0$ 决定。最终输出的质心数的范围 [$\frac{K_0}{2}$ , $2K_0$]
- 每个类所要求的最少样本数 $N_{min}$ :如果分裂后导致某个子类别包含样本数目小于 $N_{min}$,就不会进行分裂。
- 最大方差 Sigma:用于衡量某个类别中样本的分散程度。当样本的分散程度超过这个值,就进行分裂。
- 两个类别对应质心之间允许的最小距离 dmin:如果两个质心的距离小于 dmin,则需要对这两个类进行合并。
ISODATA 算法描述
- 从数据集中随机选取 $K_0$ 个样本,作为初始质心。
- 重新对样本划分类别:计算每个样本 $x_i$ ,计算它到每一个质心的距离,将其分配到距离最小质心所对应的类中。
- 判断每个类中样本数目是否小于 $N_{min}$。如果小于 $N_{min}$ 则需要丢弃该类,令 K = K - 1 ,并将该类中样本重新分配给剩下类中距离最小的类。
- 重新计算每个质心。$c_i = \frac{1}{\vert c_i \vert}\sum_{x \in c_i}x$
- 如果当前 $K <= \frac{K_0}{2} $ ,说明当前类别数太少,进行分裂
- 如果当前 $K >= 2 K_0$ ,说明当前类别数太多,进行合并
- 当满足一定条件,如类别划分不在变化时或者达到最大迭代轮数,则终止算法,否则回到第 2 步执行。
# 训练
def train(self, train_data, min_n, sigma, min_distance, k0=10, max_iter=300):
last_wcss = 0.0
iter_count = 0
centorids = np.array([train_data[i] for i in sample(range(len(train_data)), k0)])
k = k0
print("kmeans train start:", centorids)
while True:
labels = [[] for _ in range(k)]
# 聚类
wcss = self.cluster(train_data, range(len(train_data)), centorids, labels)
# 判断每个类中样本数目是否小于 N_{min}。如果小于 N_{min} 则需要丢弃该类,
# 令 K = K - 1 ,并将该类中样本重新分配给剩下类中距离最小的类。
i = 0
while i < len(labels):
if len(labels[i]) < min_n:
remove_labels = labels[i]
labels = [item for h, item in enumerate(labels) if i != h]
centorids = [item for h, item in enumerate(centorids) if i != h]
self.cluster(train_data, remove_labels, centorids, labels)
i += 1
k = len(centorids)
print("kmeans wcss:", wcss, iter_count)
# modify centers
for cluster_id in range(k):
centorids[cluster_id] = self.calc_centroid(train_data, labels[cluster_id])
# 分裂
if k <= k0 / 2:
self.split(train_data, labels, centorids, sigma, min_n)
k = len(centorids)
# 合并
if k >= 2 * k0:
print("merge")
self.merge(centorids, min_distance, labels)
k = len(centorids)
iter_count += 1
if last_wcss == wcss or iter_count == max_iter: break
last_wcss = wcss
合并
-
计算质心之间两两之间的距离,用矩阵 D 表示,其中 $D(i,i) = 0$
-
对于 $D(i,j) < d_{min}\;\;(i!=j)$ 的两个类别需要进行合并操作,变成一个新类,新类的质心:$c_{new}=\frac{1}{n_i+n_j}(n_ic_i+n_jc_j)$
$n_i\;,\;n_j$ 表示两个类别中样本数目,新的质心可以看做两个质心的加权求和。如果其中一个类所包含的样本个数较多,所合成的新质心就会更加偏向它。
# 合并
def merge(self, centorids, min_distance, lables):
k = len(centorids)
for i in range(k):
for j in range(i + 1, k):
# 计算质心之间的距离
distance = self.calc_distance(centorids[i], centorids[j])
if distance < min_distance:
n_i = len(lables[i])
n_j = len(lables[j])
# 两个质心合并为一个质心
c_new = [(n_i * centorids[i][k] + n_j * centorids[j][k]) / (n_i + n_j) for k in
range(len(centorids[i]))]
centorids = [item for h, item in enumerate(centorids) if i != h and h != j]
centorids.append(c_new)
data = lables[i] + lables[j]
lables = [item for h, item in enumerate(lables) if i != h and h != j]
lables.append(data)
分裂
- 计算每个类别下所有样本在每个维度下的方差:$s^2 = \frac{(M-x_1)^2+(M-x_2)^2+…+(M-x_n)^2}{n}$。
- 针对每个类别的所有方差挑选出最大的方差 $\sigma_{max}$。
- 如果某个类别的 $\sigma_{max}> Sigma$ 并且该类别包含样本数 $n_i >= 2n_{min}$ ,则可以分裂。
- 满足步骤 3 中条件,分裂中两个子类并令 K = K + 1. $c_i^{(+)}=c_i+\sigma_{max}\;,\; c_i^{(-)}=c_i-\sigma_{max}$
- 将类中样本重新划分中 $c_i^{(+)}\;,\;c_i^{(-)}$ 中。
# 分裂
def split(self, train_data, lables, centorids, sigma, min_n):
for i in range(len(lables)):
data = [train_data[j] for j in lables[i]]
# 计算最大方差
max_sigma = max(np.var(data, axis=0))
if not (max_sigma > sigma and len(lables[i]) >= 2 * min_n):
continue
# 新质心
c_new_0 = [v + max_sigma for v in centorids[i]]
c_new_1 = [v - max_sigma for v in centorids[i]]
tmp_lables = [[], []]
# 重新分类
self.cluster(train_data, lables[i], [c_new_0, c_new_1], tmp_lables)
# 跟新质心和聚类
centorids = [item for j, item in enumerate(centorids) if i != j]
centorids.append(c_new_0)
centorids.append(c_new_1)
lables = [item for j, item in enumerate(lables) if i != j]
lables.append(tmp_lables[0])
lables.append(tmp_lables[1])
query 聚类
query 相似度
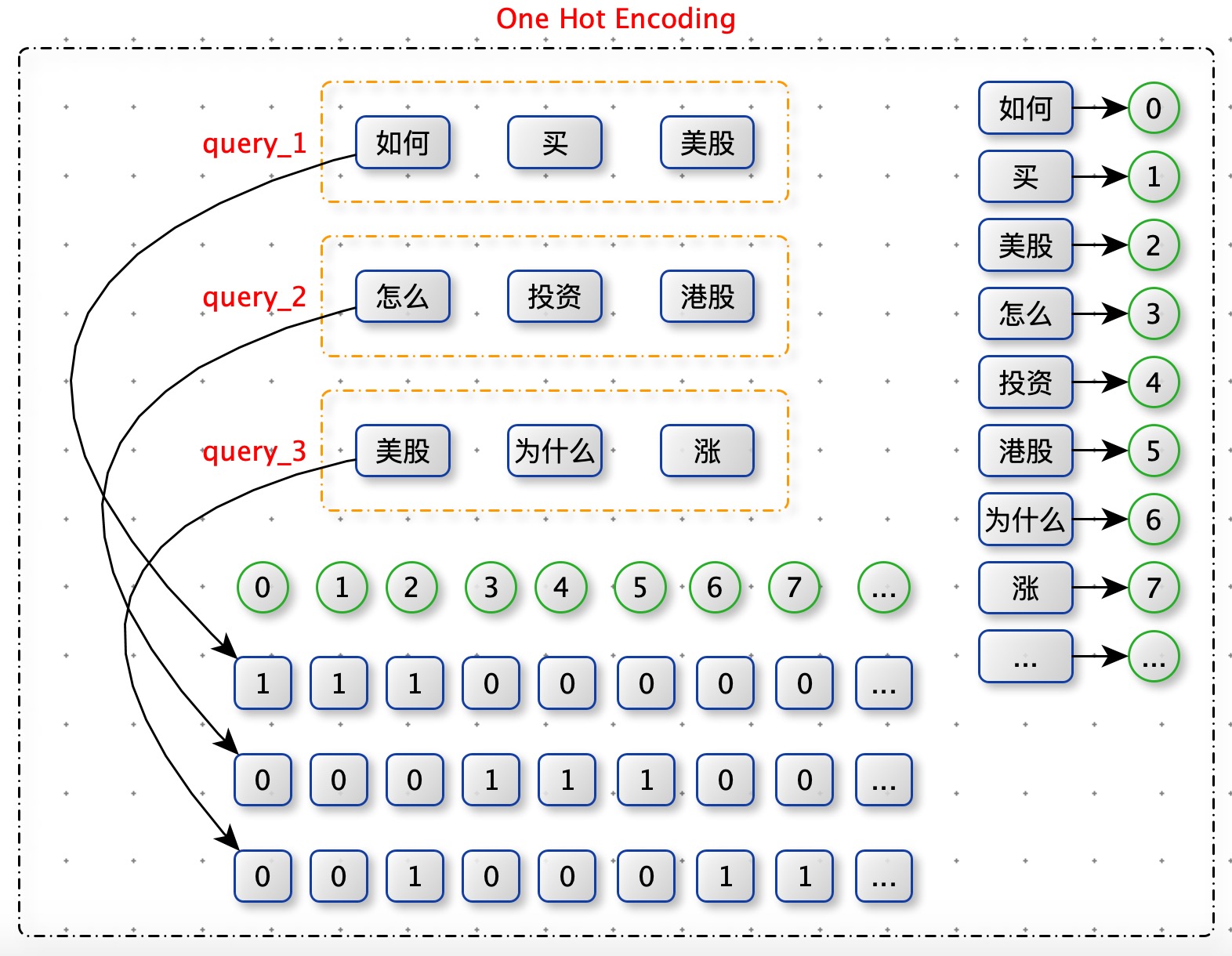
One Hot Encoding
要计算 query 与 query 的欧式距离,需要将 query 表达成高维空间中一个点。通过 One Hot Encoding。
$dist(X,Y) = \sqrt{\sum_{i=1}^n{(x_i-y_i)^2}}$
One Hot Encoding 例子:
from sklearn.preprocessing import OneHotEncoder
# handle_unknown='ignore' 忽略在 fit 中没有见过的特征值
enc = OneHotEncoder(handle_unknown='ignore')
X = [['Male', 1], ['Female', 3], ['Female', 2]]
# 生成词表
enc.fit(X)
# one-hot 编码
enc.transform([['Female', 1], ['Male', 4]]).toarray()
# 如果嫌fit 后在transform 麻烦,可以使用:enc.fit_transform(X)
$dist(X,Y) = \sqrt{\sum_{i=1}^n{(x_i-y_i)^2}}$
$dist(query_1,query_2) = \sqrt{1^2+1^2+1^2+1^2+1^2+1^2+0+…+0}=\sqrt{6}$
$dist(query_1,query_3) = \sqrt{1^2+1^2+0^2+1^2+1^2+0+…+0}=\sqrt{4}$
$\sqrt{6}>\sqrt{4}$ 所以query_1 与 query_3 距离更短,更相似。这与我们感觉不相符?Why?
因为:One Hot Encoding 认为维度与维度是独立的,会造成信息的丢失。
query 本身就很短,信息量很少,我们要充分利用这些少的可怜的信息,不能再独立的假设了。
如何 -> 怎么 -> 0 -> ?
投资 -> 买 -> 0 -> ?
美股 -> 港股 -> 0 -> ?
怎么办计算词与词的相似度(距离)?
word2vec
$dist(X,Y) = \sqrt{\sum_{i=1}^n{(x_i-y_i)^2}}$
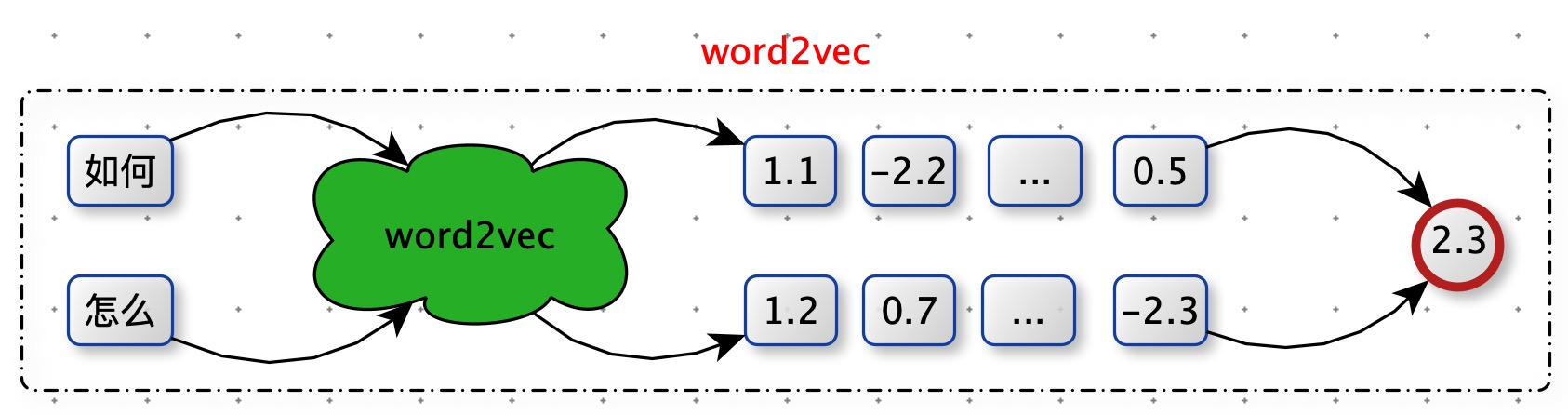

训练 word2vec 模型
nohup word2vec -train train_data_file_name -output vec_model_file_name -size 100 -window 5 -sample 1e-3 -negative 5 -hs 0 -binary 0 -cbow 1 -iter 5 &
参数说明:
- train:语料集,建议使用 BrownCorpus , Text8Corpus 或 ·ineSentence 构建。
- output:模型文件名
- size:是指特征向量的维度,默认为100。大的size需要更多的训练数据,但是效果会更好. 推荐值为几十到几百。
- window:表示当前词与预测词在一个句子中的最大距离是多少。Harris 在 1954 年提出的分布假说( distributional hypothesis)指出, 一个词的词义由其所在的上下文决定。所以word2vec的参数中,窗口设置一般是5,而且是左右随机1-5(小于窗口大小)的大小,是均匀分布,随机的原因应该是比固定窗口效果好,增加了随机性,个人理解应该是某一个中心词可能与前后多个词相关,也有的词在一句话中可能只与少量词相关(如短文本可能只与其紧邻词相关)。
- sample:高频词汇的随机降采样的配置阈值,默认为1e-3,范围是(0,1e-5)。
- negative:如果>0,则会采用negativesamp·ing,用于设置多少个noise words。
- hs:如果为1则会采用hierarchica·softmax技巧。如果设置为0(defau·t),则negative sampling会被使用。
- binary:为1指的是结果二进制存储,为0是普通存储。
- cbow:如果为0,则采用上下文词向量的和,如果为1(defau·t)则采用均值。只有使用CBOW的时候才起作用。
- iter: 迭代次数,默认为 5。
训练数据
- 雪球帖子数据:1.3G,700838 条 + 用户( 1894299685 )的所有帖子 +用户( 5507081370 ) 的长帖
- 维基百科数据:1.2 G,372433 条
- 智齿系统用户反馈问题数据:544 条
有了 word 与 word 之间相似度,怎么计算 query 与 query 的相似度?
第一版:选择词相关性最大分值,求和。
如下图:query1 = “如何买美股” 和 query2= “怎么投资港股”。
- 分词:对 query1 分词后得到 [“如何”,“买”,“美股”],query2 分词后得到 [“怎么”,“投资”,“港股”]。
- 计算词与词的相似度:使用 word2vec 分别计算 “如何” 与 [“怎么”,“投资”,“港股”] 的相似度,选取最大值作为 “如何” 对应的分值 s1。
- 计算 query 与 query 的相似度:s = s1 + s2 + s3
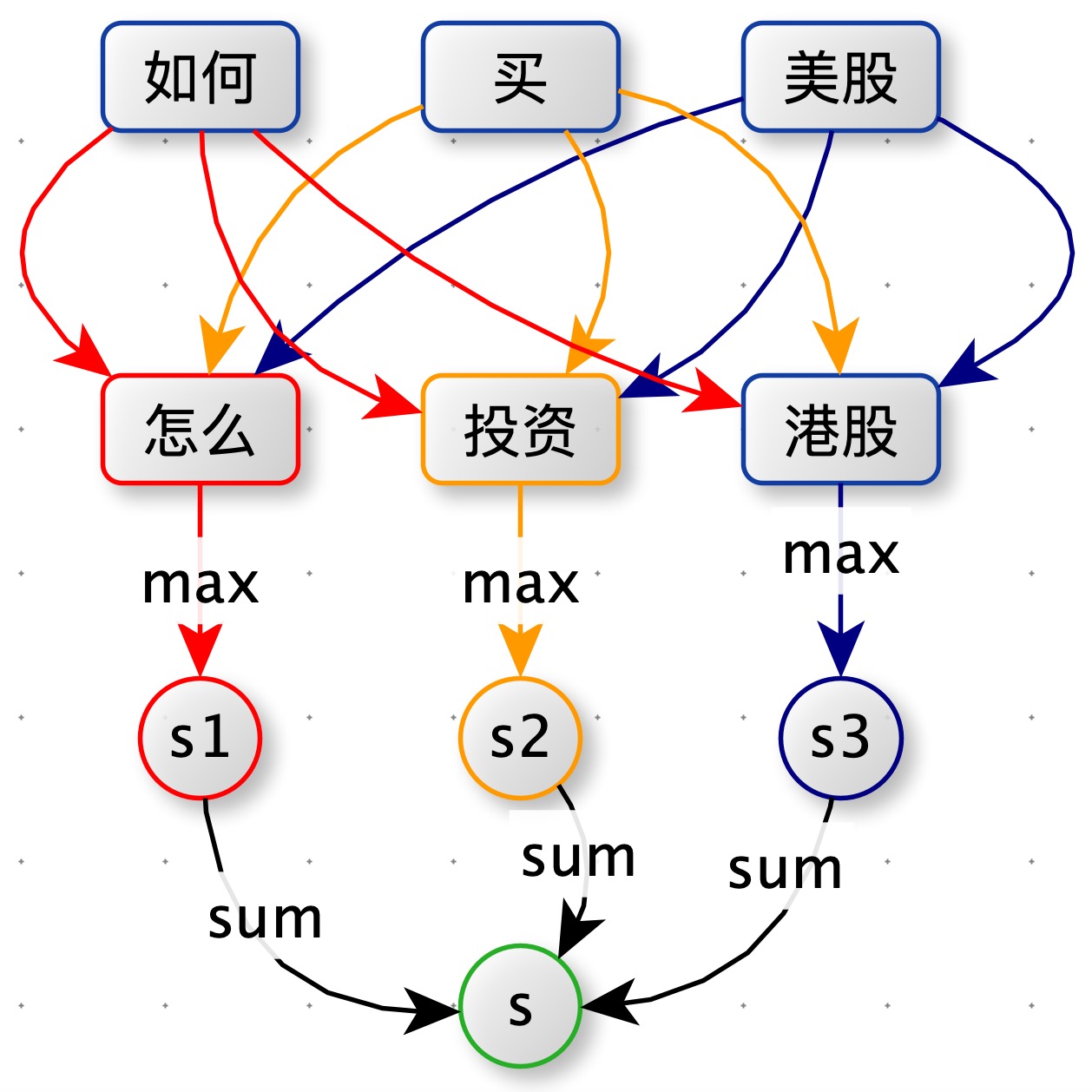
第二版:添加词性约束
如下图所示,在第一版方案中:原本预期:(“如何”,“怎么”)、(“买”,“投资”)、(“美股”,“港股”)之间相似度最大,但实际上(“买”,“港股”)的相似度最大。“买港股” 确实在训练 word2vec 的语料中经常出现。为了达到预期的目标,我们添加了词性约束。

新增词性约束
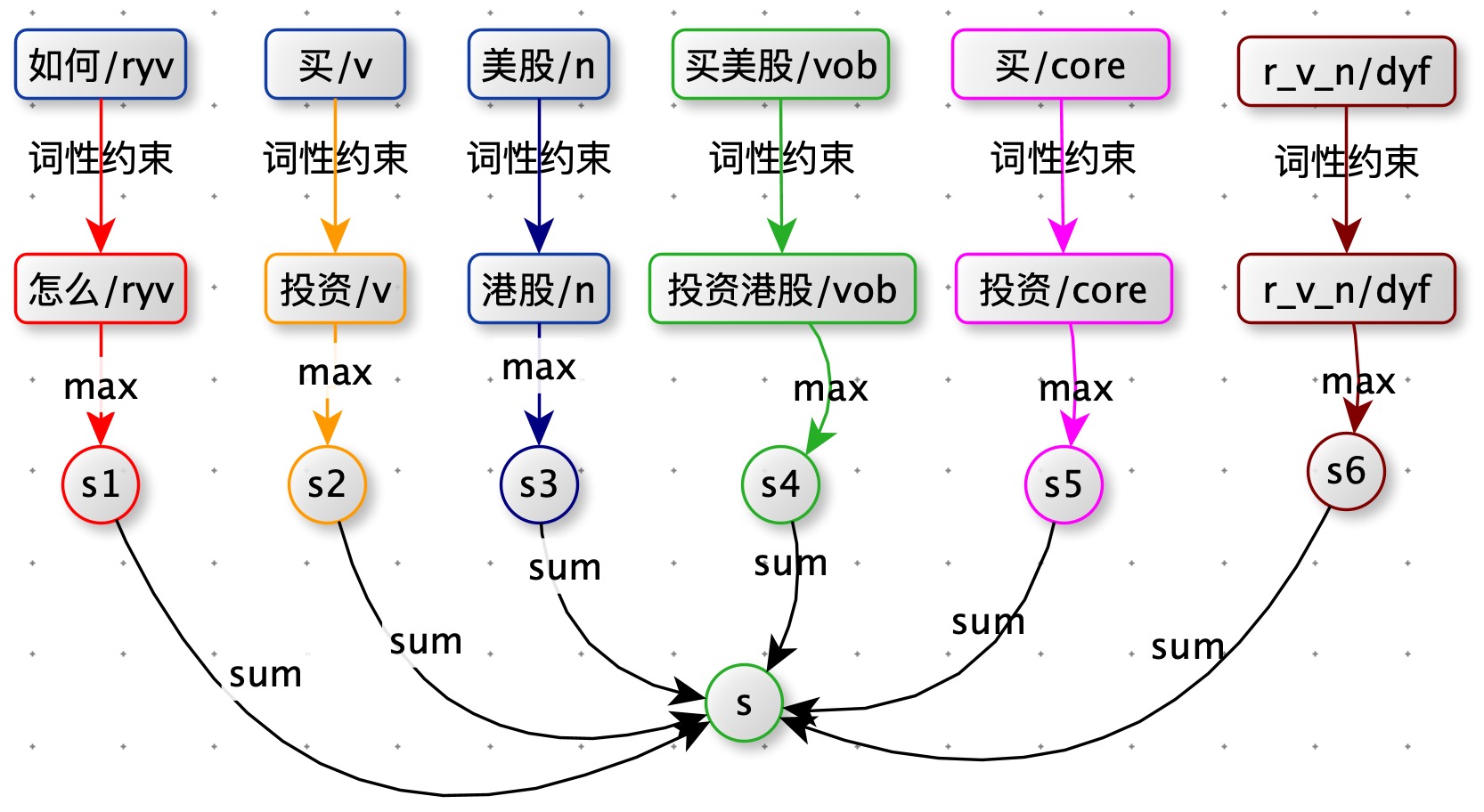
如下图:query 分完词后,都带有词性。计算词与词的相似度时,方案一中是将 query1 中的一个单词与 query2 中所有单词都计算相似度。本方案优化为:将 query1 中的一个单词只与 query2 中词性相同的单词计算相似度(如果有多个取最大值那个)。例如:query1 中 “如何” 只与 query2 中的 “怎么” 计算相似度。
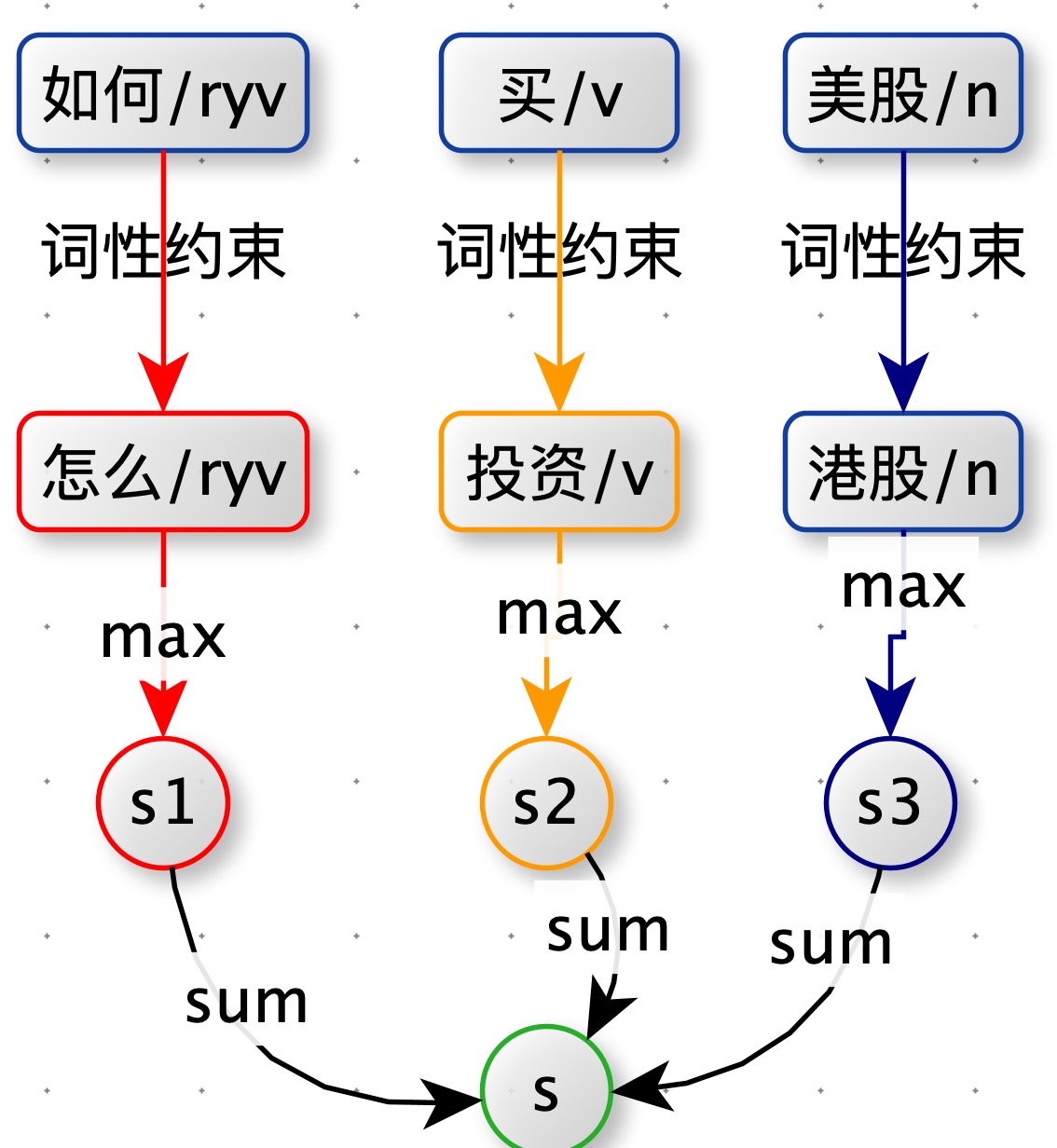
第三版:扩展核心词,动宾结构,句式结构,有股票名称新增:xx_stock
为了提高相似 query 与 query 之间的相似度分值,新增了一些特征:
- query 的核心词
- 动宾结构:query 一般很短,如果query1 和 query2 中都有动宾结构,那么动宾结构大概率是用户搜索意图,是非常重要的特征。
- query 所有词的词性:为了将相似的句式的 query 聚合在一起。
- query 中的股票:query 中股票也是用户强烈的搜索意图。
处理完毕的 query

相同句式的 query

query 与 query 相似度代码:
def similarity_sentence(self, sentence1, sentence2):
similarity = 0.0
for word in sentence1:
max_word, max_score = self.max_word(word, sentence2)
similarity += max_score
return similarity / len(sentence1)
def max_word(self, word, sentence):
max_score = 0
max_word = ""
w, p = word
for w2, p2 in sentence:
if p2 != p: continue
score = self.similarity_word(w, w2)
if score is None: continue
if max_score < score:
max_score = score
max_word = w2
return (max_word, max_score)
def similarity_word(self, word1, word2):
if word1 not in self.word2vec_model.keys():
self.log.write(word1 + " not in model\n")
return
if word2 not in self.word2vec_model.keys():
self.log.write(word2 + " not in model\n")
return
vec1 = self.word2vec_model[word1]
vec2 = self.word2vec_model[word2]
prod = 0
mod1 = 0
mod2 = 0
for i in range(min(len(vec2), len(vec2))):
prod += vec1[i] * vec2[i]
mod1 += vec1[i] * vec1[i]
mod2 += vec2[i] * vec2[i]
return prod / (math.sqrt(mod1) * math.sqrt(mod2))
至此能够按照业务想要的方式计算 query 与 query 的相关性。
问题:怎么将定制相关性计算,融合到 KMeans 中?
定制 KMeans
KMeans 核心步骤:
- 重新对样本划分类别:计算每个样本 $x_i$ ,计算它到每一个质心的距离,将其分配到距离最小质心所对应的类中。
- 重新计算每个质心。$c_i = \frac{1}{\vert c_i \vert }\sum_{x \in c_i}x$
替换距离计算
将第一步中距离计算,替换为query 与 query 相似度计算。
虚质心改为实质心
计算质心麻烦:质心是虚拟的点(不是样本点),无法找到质心对应词,没有词就没有办法通过word2vec 计算词与词的距离,进而无法计算 query 与质心的距离(相似度)。
例如:绿色类中点:$A:[x_1,y_1] \,, B:[x_2,y_2]\,,C:[x_3,y_3]\,,D:[x_4,y_4]$
更新绿色质心:$[\frac{x_1+x_2+x_3+x_4}{4},\frac{y_1+y_2+y_3+y_4}{4}]$
**注意:此时的质心是虚拟的点(不是训练集中的样本)**
解决方案:强制让质心是训练集中的样本点。
问题:在一个类别,选择哪一个样本点作为质心?
答:最靠近中心的样本点,最为质心最合适。
问题:怎么选出来最靠近中心的样本点?或者说最靠近中心的样本点有什么特征?
答:在一个类别中,计算每个样本点到其他样本点的距离之和,最靠近中心的样本点距离之和最小。

# 计算质心
def calc_centroid(self, data):
max_wcss = -100
result = -1
for i in data:
wcss = 0
for j in data:
wcss += self.similarity_map[(i, j)]
if max_wcss < wcss:
result = i
max_wcss = wcss
return result
注意:时间复杂度为:$O(n^2)$。在训练之前计算所有 query 与 query 的相似度保存在字典中,后续所有用到地方,直接获取。
其他改进
- 实现了KMeans ++ :优化质心初始化。
- 加入质心过滤规则:query 小于 3个词,大于10个词,不包含一个动词和一个名词。
- 多轮迭代聚类:指定一个最小相似度(min_similarity),一次聚类完成后,自动将相似度小于 min_similarity 的样本过滤出来,进行下一次的聚类。
完整代码:
# coding:utf-8
# kmeans 对 query 聚类:自定义 query 与 query 的相似度。
# query 与 query 的相似度:sum(word2vec * word2vec)
import math
from random import sample
class MyKmeans:
def __init__(self, train_data_file_name, n_clusters=10, max_iter=300,min_similarity=0.5):
self.n_clusters = n_clusters
self.max_iter = max_iter
self.word2vec_model = None
self.train_data = {}
self.similarity_map = None
self.centers = []
self.labels = set()
self.dir_path = "./"
self.train_file_name = train_data_file_name
self.log = open(self.dir_path + train_data_file_name + "_log.log", "w")
self.centers_black_list = set()
self.min_similarity = min_similarity
print('kmeans loading word2vec model')
self.load_word2vec_model(self.dir_path + "vec_model_v3")
print('kmeans loaded word2vec model')
print('kmeans loading train data')
self.load_train_data(self.dir_path + self.train_file_name)
print('kmeans loaded train data')
self.init_center()
def __del__(self):
self.log.close()
def load_word2vec_model(self, model_file_name):
model = {}
for line in open(model_file_name, "r"):
try:
data = line.strip().split(" ")
if len(data) < 2: continue
model[data[0]] = [float(x) for x in data[1::]]
except Exception as err:
print(err, line)
self.word2vec_model = model
# 数据格式:
# 如何/ryv 看盘/v
def load_train_data(self, file_name):
train_data = {}
i = 0
for line in open(file_name):
try:
train_data[i] = [(item.strip().split("/")[0], item.strip().split("/")[1]) for item in line.strip().split(" ") if
len(item) > 0 and len(item.strip().split("/")) > 1]
i += 1
except Exception as err:
print(err, line, "kmeans")
self.train_data = train_data
def init_center(self):
center_black_list = set()
for sid,item in self.train_data.items():
if len(item) < 3 or len(item)>10:center_black_list.add(sid)
pos_tag_v = [(w,p) for w,p in item if p == "v" ]
pos_tag_n = [(w,p) for w,p in item if p.find("n") == 0 ]
if len(pos_tag_v) == 0 or len(pos_tag_n) == 0:center_black_list.add(sid)
self.center_black_list = center_black_list
# 初始化质心
self.centers = sample( [ sid for sid,item in self.train_data.items() if sid not in center_black_list ], self.n_clusters)
# 训练
def train(self,calc_similarity=False):
print("kmeans calc all similarity start")
if not self.similarity_map:
if calc_similarity:
self.calc_train_data_similarity()
else:
self.load_similarity_map()
last_wcss = 0.0
iter_count = 0
print("kmeans train start")
while True:
self.labels = set([[sid] for sid in self.centers])
wcss = 0
for sid,feature in self.train_data.items():
max_similarity = -100
cluster = -1
for i, centroid_id in enumerate(self.centers):
if max_similarity < self.similarity_map[(sid, centroid_id)]:
max_similarity = self.similarity_map[(sid, centroid_id)]
cluster = i
self.labels[cluster].add(sid)
wcss += max_similarity
print("kmeans wcss:", wcss, iter_count)
# modify centers
for i in range(self.n_clusters):
new_centers = self.calc_centroid(self.labels[i])
if new_centers >= 0:
self.centers[i] = new_centers
iter_count += 1
if last_wcss == wcss or iter_count == self.max_iter: break
last_wcss = wcss
print("kmeans train Over")
# 计算质心
def calc_centroid(self, data):
max_wcss = -100
result = -1
for sid in data:
if sid in self.center_black_list:continue
wcss = 0
for sid2 in data:
if sid2 in self.center_black_list:continue
wcss += self.similarity_map[(sid, sid2)]
if max_wcss < wcss:
result = sid
max_wcss = wcss
return result
def calc_train_data_similarity(self):
similarity_map = {}
k = 0
for sid,feature in self.train_data.items():
for sid2,feature2 in self.train_data.items():
k += 1
if k % 10000 == 0:
print("kmeans calc_train_data_similarity:", k)
similarity_map[(sid, sid2)] = self.similarity_sentence(feature, feature2)
self.similarity_map = similarity_map
self.save_similarity()
def similarity_sentence(self, sentence1, sentence2):
similarity = 0.0
for word in sentence1:
max_word, max_score = self.max_word(word, sentence2)
similarity += max_score
return similarity / len(sentence1)
def max_word(self, word, sentence):
max_score = -1.0
max_word = ""
w, p = word
for w2, p2 in sentence:
if p2 != p: continue
score = self.similarity_word(w, w2)
if score is None: continue
if max_score < score:
max_score = score
max_word = w2
return (max_word, max_score)
def similarity_word(self, word1, word2):
if word1 == word2:
return 1.0
if word1 not in self.word2vec_model.keys():
self.log.write(word1 + " not in model\n")
return
if word2 not in self.word2vec_model.keys():
self.log.write(word2 + " not in model\n")
return
vec1 = self.word2vec_model[word1]
vec2 = self.word2vec_model[word2]
prod = 0
mod1 = 0
mod2 = 0
for i in range(min(len(vec2), len(vec2))):
prod += vec1[i] * vec2[i]
mod1 += vec1[i] * vec1[i]
mod2 += vec2[i] * vec2[i]
return prod / (math.sqrt(mod1) * math.sqrt(mod2))
def save_model(self,i):
fw_next_train_data = open(self.dir_path + self.train_file_name+"_train_data_"+str(i),"w")
fw = open(self.dir_path + self.train_file_name + "_model_"+str(i), "w")
# 存质心
fw.write(",".join([str(x) for x in self.centers]) + "\n")
# 存分类
for i in range(len(self.labels)):
fw.write(str(self.labels[i]) + "\n")
next_train_data = {}
for label in range(len(self.labels)):
for score,sid in sorted([ (self.similarity_map[(self.centers[label],sid)],sid) for sid in self.labels[label] ],reverse=True):
if score < self.min_similarity:
fw_next_train_data.write(" ".join([ w+ "/"+p for w,p in self.train_data[sid] ] )+"\n")
next_train_data[sid] = self.train_data[sid]
else:
fw.write(str(label)+","+str(sid)+","+str(score)+","+str(self.train_data[sid])+"\n")
self.train_data = next_train_data
fw.close()
fw_next_train_data.close()
def save_similarity(self):
fw = open(self.dir_path + self.train_file_name + "_similarity", "w")
for k, v in self.similarity_map.items():
fw.write(str(k) + "," + str(v) + "\n")
fw.close()
# (1531, 3553),-0.2741255043304492
def load_similarity_map(self):
similarity_map = {}
for line in open(self.dir_path + self.train_file_name + "_similarity", "r"):
data = line.replace('(','').replace(')','').replace(' ','').strip().split(',')
if len(data) != 3:continue
similarity_map[(int(data[0]),int(data[1]))] = float(data[2])
self.similarity_map = similarity_map
def multi_iter_train(self):
print("第 0 轮 start")
self.train()
self.save_model(0)
# self.save_similarity()
print("第 0 轮 end")
for i in range(9):
print("第"+str(i+1)+" 轮 start")
if (len(self.train_data) - len(self.center_black_list)) <= self.n_clusters:break
self.init_center()
self.train()
self.save_model(i+1)
print("第"+str(i+1)+" 轮 start")
my_kmeans = MyKmeans("all_query_3docker_uniq_rvn_text_seg_filter", n_clusters=100,min_similarity=0.4)
my_kmeans.multi_iter_train()
print("Over")
聚类结果
类一:股票的某一个指标怎么看

类二:最近行情为什么涨(跌)

类三:某一只股票为什么涨(跌)

类四:跟打新相关的操作
