平衡性
- 每棵子树的大小,不小于其兄弟的子树大小。既每棵叔叔树的大小,不小于其任何侄子树的大小。
左旋
触发条件:cur = 节点 4,cur.right.right.size > cur.left.size。出现右边子树节点数太多。通过左旋,将 cur.right 的结点替换 cur 节点。
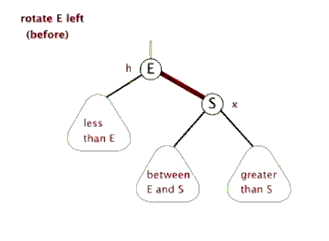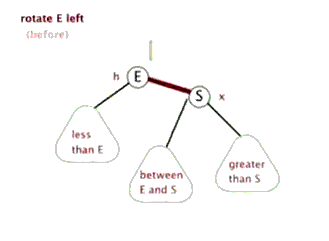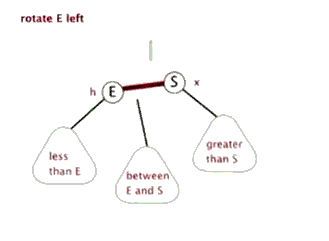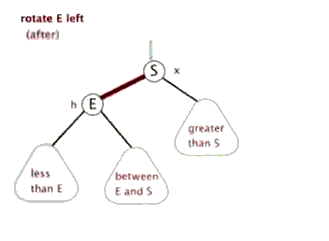
具体过程如下图
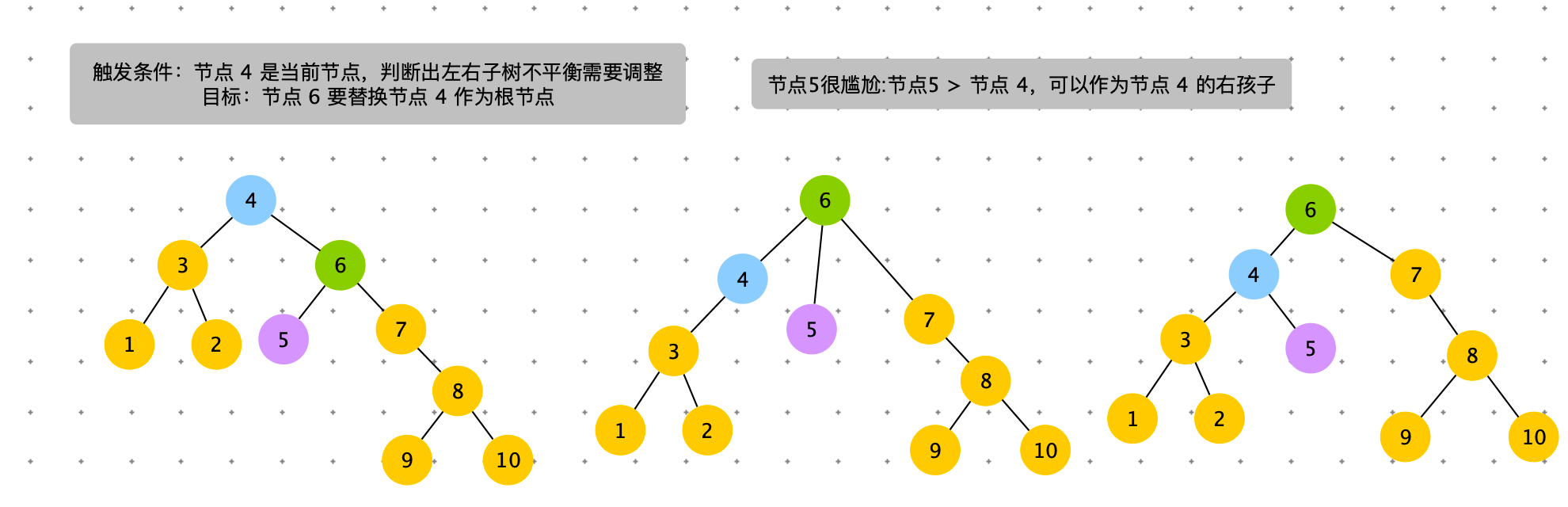
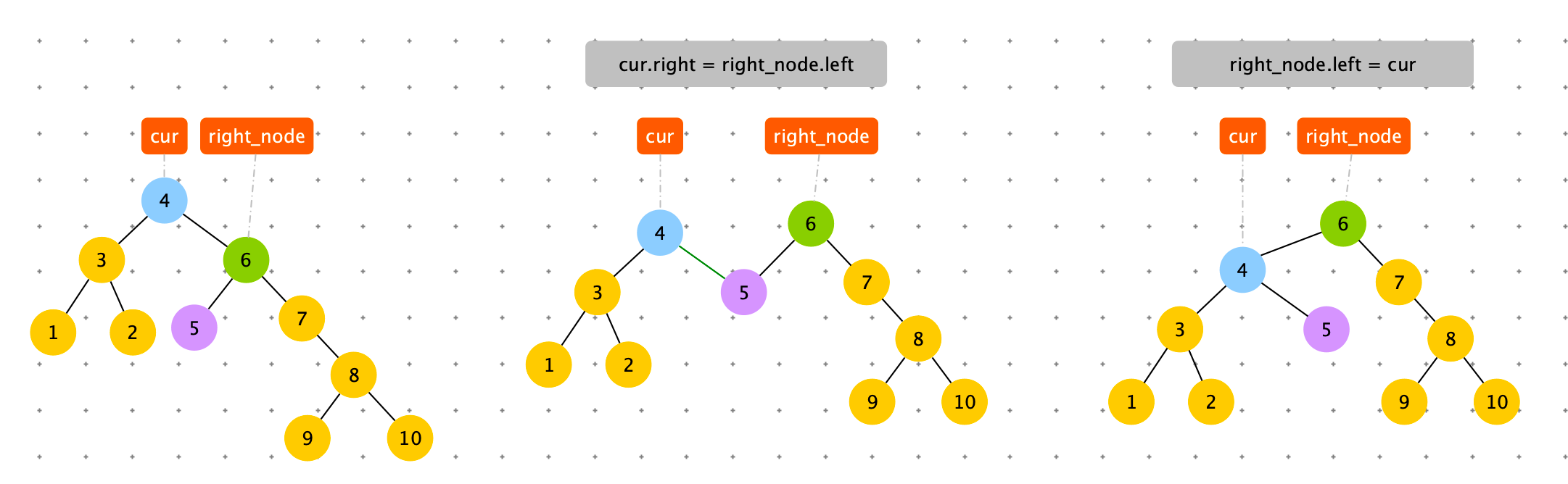
# 左旋
def left_rotate(self, cur: Node):
right_node = cur.right
cur.right = right_node.left
right_node.left = cur
# 此时 right_node 成为父节点
right_node.size = cur.size
cur.size = (cur.left.size if cur.left else 0) + (cur.right.size if cur.right else 0) + 1
return right_node
if right_right_size > left_size: # 左旋
cur = self.left_rotate(cur)
cur.left = self.maintain(cur.left)
cur = self.maintain(cur)
右旋
触发条件:cur = 节点 4,cur.left.left.size > cur.right.size。出现左边子树节点数太多。通过右旋,将 cur.left 的结点替换 cur 节点。
具体过程如下图
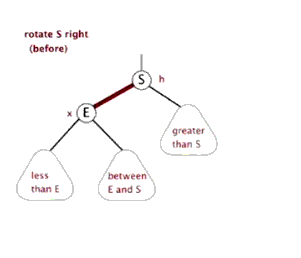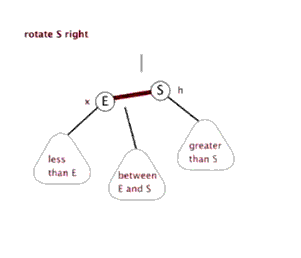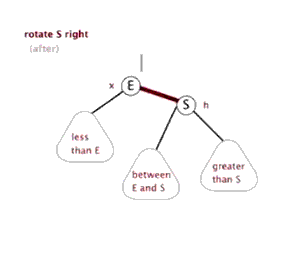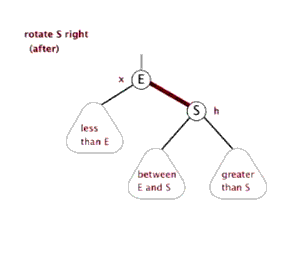
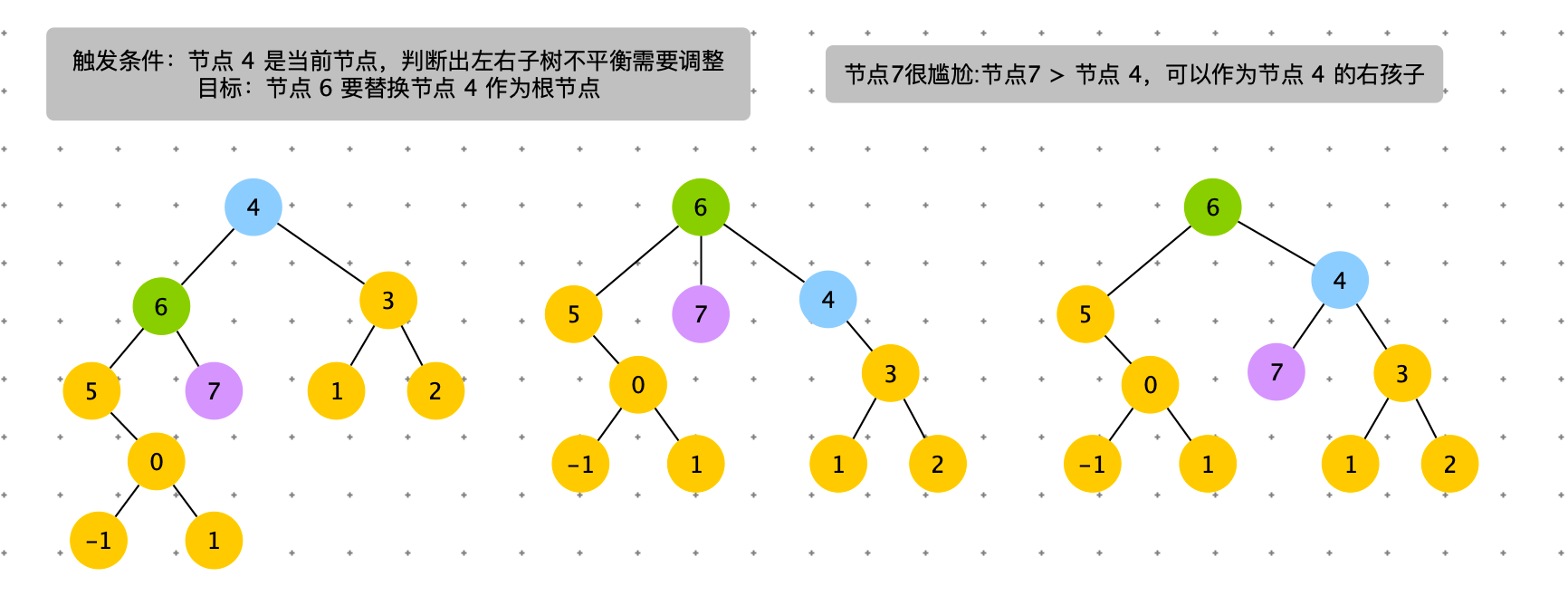

# 右旋
def right_rotate(self, cur: Node):
left_node = cur.left
cur.left = left_node.right
left_node.right = cur
# 此时 left_node 成为父节点
left_node.size = cur.size
cur.size = (cur.left.size if cur.left else 0) + (cur.right.size if cur.right else 0) + 1
return left_node
# 右旋
if left_left_size > right_size:
cur = self.right_rotate(cur)
cur.right = self.maintain(cur.right)
cur = self.maintain(cur)
左旋 + 右旋
触发条件:cur = 节点 4,cur.left.right.size > cur.right.size。出现左边子树节点数太多。通过右旋,将 cur.left 的结点替换 cur 节点。
具体过程如下图
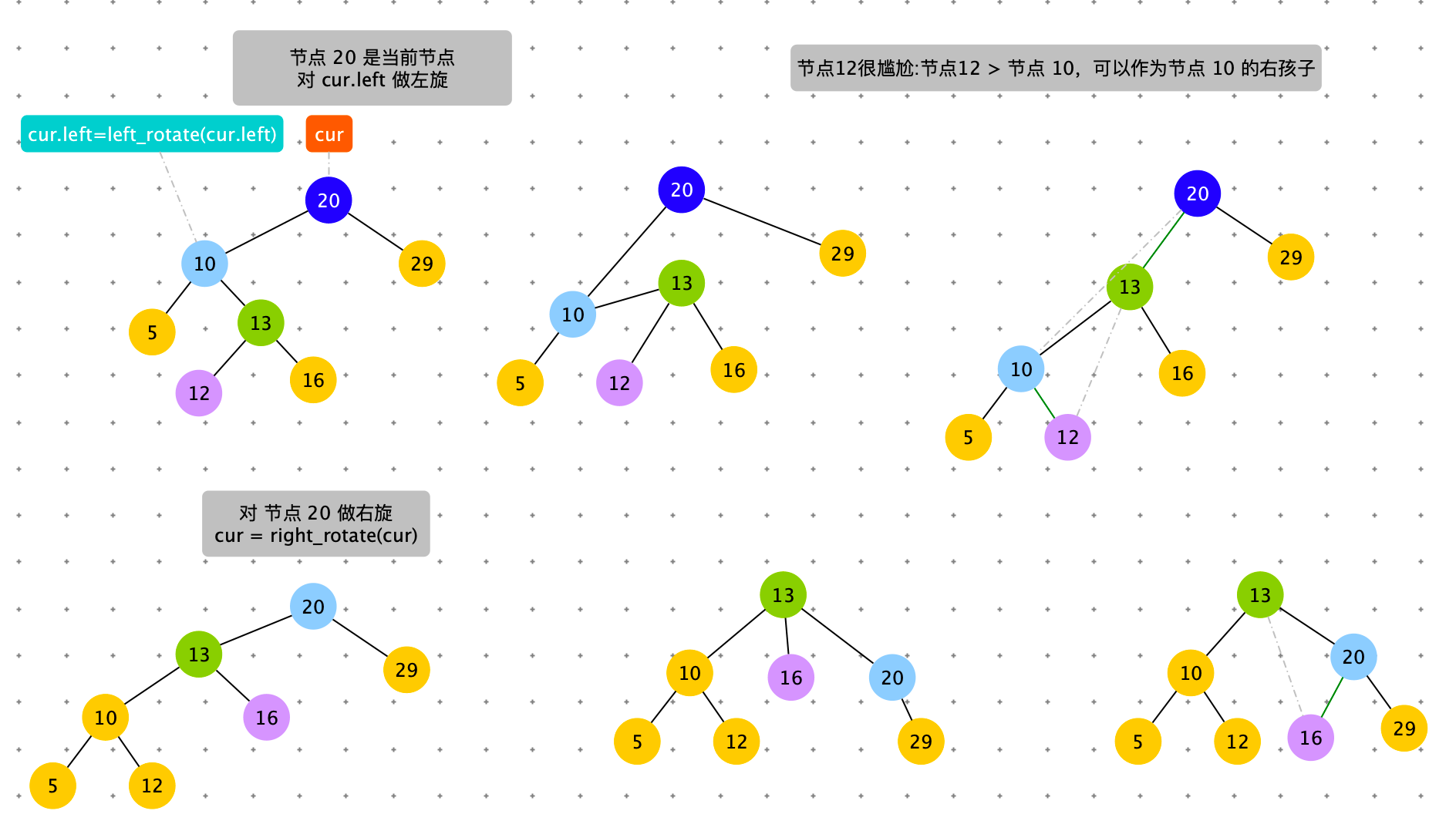
if left_right_size > right_size: # 左旋,右旋
cur.left = self.left_rotate(cur.left)
cur = self.right_rotate(cur)
# 检查cur.left 是否平衡
cur.left = self.maintain(cur.left)
# 检查cur.right 是否平衡
cur.right = self.maintain(cur.right)
cur = self.maintain(cur)
右旋 + 左旋
触发条件:cur = 节点 4,cur.right.left.size > cur.left.size。出现左边子树节点数太多。通过右旋,将 cur.left 的结点替换 cur 节点。
具体过程如下图
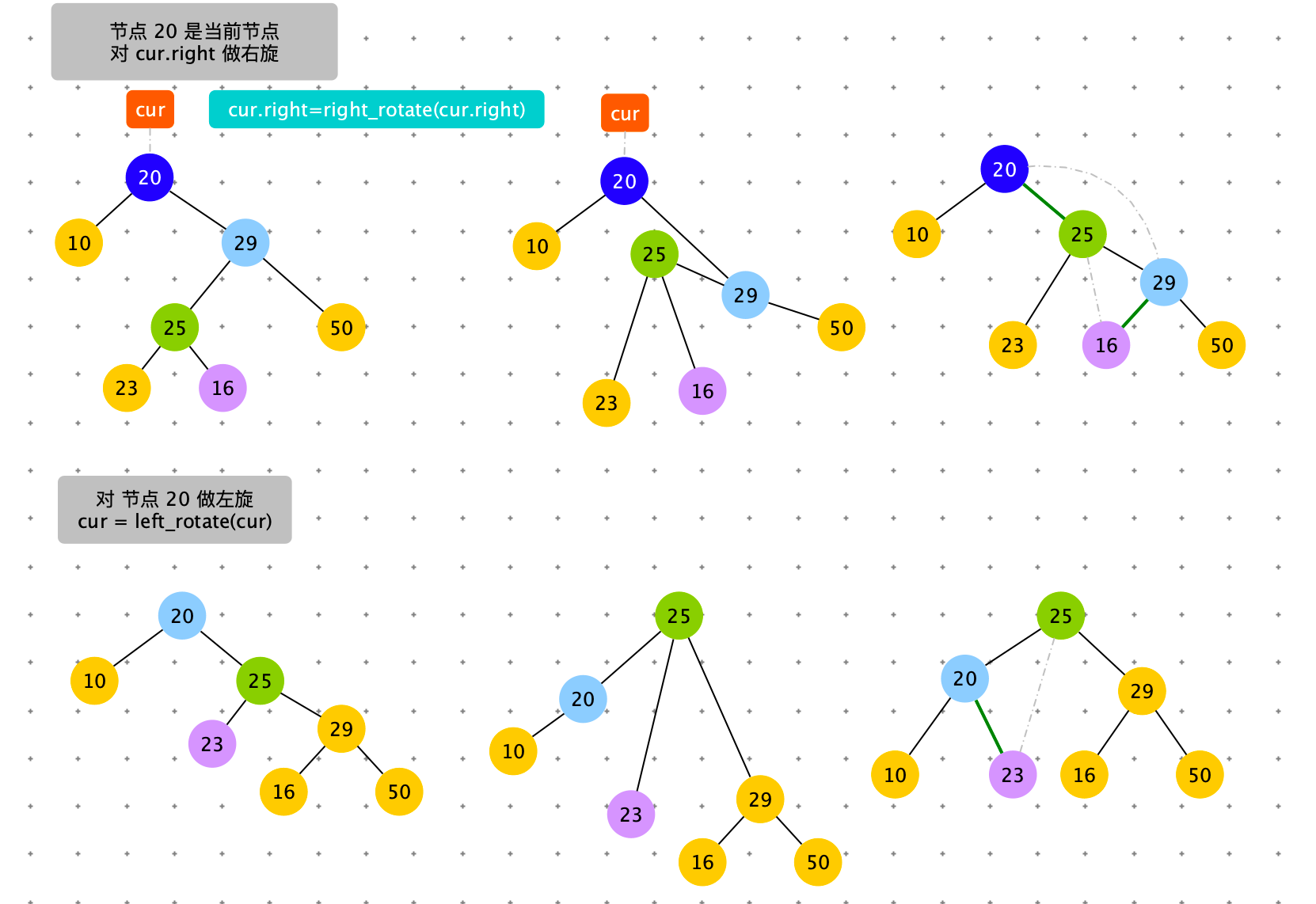
if right_left_size > left_size: # 右旋,左旋
cur.right = self.right_rotate(cur.right)
cur = self.left_rotate(cur)
cur.left = self.maintain(cur.left)
cur.right = self.maintain(cur.right)
cur = self.maintain(cur)
删除
删除节点为叶子节点

删除节点有left 节点,没有 right 节点:cur = cur.left
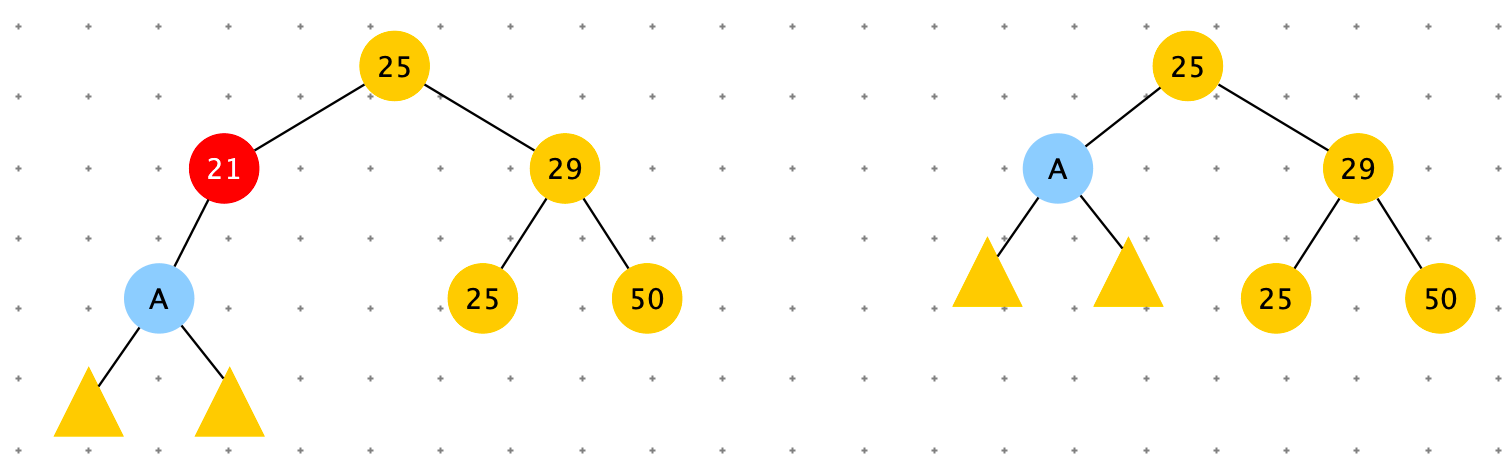
删除节点有 right节点,没有 left节点:cur = cur.right

删除节点 21。cur 有左节点和右节点。用cur.left 的最右节点替换 cur 或者使用 cur.right 的最左节点替换 cur。
下图是用 cur.right 的最左节点替换 cur。 下图 des.left 为空,需要安排好 desc.right , pre.left = desc.right
替换: des.left = cur.left ; des.right = cur.right。
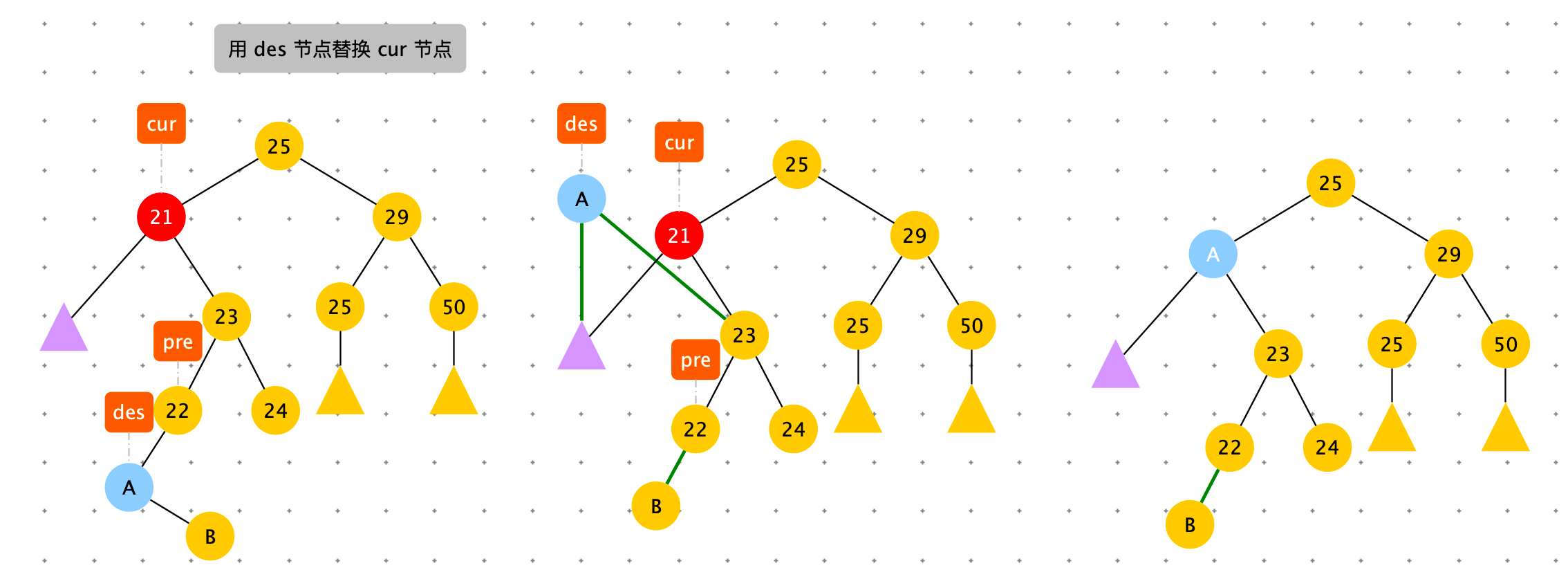
# 在cur这棵树上,删掉 key 所代表的节点
# 返回cur这棵树的新头部
def delete(self, cur: Node, key):
cur.size -= 1
if cur.key > key:
cur.left = self.delete(cur.left, key)
elif cur.key < key:
cur.right = self.delete(cur.right, key)
else:
# 要删除 cur,cur.key == key
# cur 是叶子节点
if not cur.left and not cur.right:
cur = None
# cur 只有右节点
elif not cur.left and cur.right:
cur = cur.right
# cur 只有左节点
elif cur.left and not cur.right:
cur = cur.left
else:
# cur 有左有右
# 查询到 cur.right 的最左边的结点 pre
# 可以替换 cur 的节点为:cur.right 的最左节点或者 cur.left 最右节点
pre = None
des = cur.right
des.size -= 1
while not des.left:
pre = des
des = des.left
des.size -= 1
if pre:
# 将 des.right 安排给好的人家
pre.left = des.right
# des.right 替换 cur.right
des.right = cur.right
# des.left 替换 cur.left
# des 替换 cur 完毕
des.left = cur.left
# 更新 des
des.size = des.left.size + (des.right.size if des.right else 0) + 1
cur = des
return cur
class Node:
def __init__(self, key, value):
self.key = key
self.value = value
self.size = 1
self.left = None
self.right = None
class SizeBalancedTreeMap:
def __init__(self):
self.root: Node = None
# 右旋
def right_rotate(self, cur: Node):
left_node = cur.left
cur.left = left_node.right
left_node.right = cur
# 此时 left_node 成为父节点
left_node.size = cur.size
cur.size = (cur.left.size if cur.left else 0) + (cur.right.size if cur.right else 0) + 1
return left_node
# 左旋
def left_rotate(self, cur: Node):
right_node = cur.right
cur.right = right_node.left
right_node.left = cur
# 此时 right_node 成为父节点
right_node.size = cur.size
cur.size = (cur.left.size if cur.left else 0) + (cur.right.size if cur.right else 0) + 1
return right_node
def maintain(self, cur: Node):
if not cur: return
left_size = cur.left.size if cur.left else 0
left_left_size = cur.left.left.size if cur.left and cur.left.left else 0
left_right_size = cur.left.right.size if cur.left and cur.left.right else 0
right_size = cur.right.size if cur.right else 0
right_right_size = cur.right.right.size if cur.right and cur.right.right else 0
right_left_size = cur.right.left.size if cur.right and cur.right.left else 0
# 右旋
if left_left_size > right_size:
cur = self.right_rotate(cur)
cur.right = self.maintain(cur.right)
cur = self.maintain(cur)
elif left_right_size > right_size: # 左旋,右旋
cur.left = self.left_rotate(cur.left)
cur = self.right_rotate(cur)
cur.left = self.maintain(cur.left)
cur.right = self.maintain(cur.right)
cur = self.maintain(cur)
elif right_right_size > left_size: # 左旋
cur = self.left_rotate(cur)
cur.left = self.maintain(cur.left)
cur = self.maintain(cur)
elif right_left_size > left_size: # 右旋,左旋
cur.right = self.right_rotate(cur.right)
cur = self.left_rotate(cur)
cur.left = self.maintain(cur.left)
cur.right = self.maintain(cur.right)
cur = self.maintain(cur)
return cur
def find_last_index(self, key):
pre = self.root
cur = self.root
while cur:
pre = cur
if cur.key == key:
return pre
if cur.key > key:
cur = cur.left
else:
cur = cur.right
return pre
def find_last_no_small_index(self, key):
res = None
cur = self.root
while cur:
if cur.key == key:
return cur
if cur.key > key:
res = cur
cur = cur.left
else:
cur = cur.right
return res
def find_last_no_big_index(self, key):
res = None
cur = self.root
while cur:
if cur.key == key:
return cur
if cur.key > key:
cur = cur.left
else:
res = cur
cur = cur.right
return res
# 现在,以cur为头的树上,新增,加(key, value)这样的记录
# 加完之后,会对cur做检查,该调整调整
# 返回,调整完之后,整棵树的新头部
def add(self, cur: Node, key, value):
if not cur: return Node(key, value)
# 寻找插入点
cur.size += 1
if cur.key > key:
cur.left = self.add(cur.left, key, value)
else:
cur.right = self.add(cur.right, key, value)
# 调整平衡性
return self.maintain(cur)
# 在cur这棵树上,删掉 key 所代表的节点
# 返回cur这棵树的新头部
def delete(self, cur: Node, key):
cur.size -= 1
if cur.key > key:
cur.left = self.delete(cur.left, key)
elif cur.key < key:
cur.right = self.delete(cur.right, key)
else:
# 要删除 cur,cur.key == key
# cur 是叶子节点
if not cur.left and not cur.right:
cur = None
# cur 只有右节点
elif not cur.left and cur.right:
cur = cur.right
# cur 只有左节点
elif cur.left and not cur.right:
cur = cur.left
else:
# cur 有左有右
# 查询到 cur.right 的最左边的结点 pre
# 可以替换 cur 的节点为:cur.right 的最左节点或者 cur.left 最右节点
pre = None
des = cur.right
des.size -= 1
while not des.left:
pre = des
des = des.left
des.size -= 1
if pre:
# 将 des.right 安排给好的人家
pre.left = des.right
# des.right 替换 cur.right
des.right = cur.right
# des.left 替换 cur.left
# des 替换 cur 完毕
des.left = cur.left
# 更新 des
des.size = des.left.size + (des.right.size if des.right else 0) + 1
cur = des
return cur
def get_index(self, cur: Node, kth):
left_size = cur.left.size if cur.left else 0
if kth == left_size + 1:
return cur
elif kth <= left_size:
return self.get_index(cur.left, kth)
return self.get_index(cur.right, kth - left_size - 1)
def size(self):
return self.root.size if self.root else 0
def __contains__(self, key):
if not key: return
last_node = self.find_last_index(key)
return last_node and last_node.key == key
def put(self, key, value):
if not key: return
last_node = self.find_last_index(key)
if last_node and last_node.key == key:
last_node.value = value
else:
self.root = self.add(self.root, key, value)
def remove(self, key):
if not key: return key
if self.__contains__(key):
self.root = self.delete(self.root, key)
def get_index_key(self, index):
if index < 0 or index >= self.root.size: return
return self.get_index(self.root, index + 1).key
def get_index_value(self, index):
if index < 0 or index >= self.root.size: return
return self.get_index(self.root, index + 1).value
def get(self, key):
if not key: return
last_node = self.find_last_index(key)
if last_node and last_node.key == key:
return last_node.value
def first_key(self):
if not self.root: return
cur = self.root
while cur.left:
cur = cur.left
return cur.key
def last_key(self):
if not self.root: return
cur = self.root
while cur.right:
cur = cur.right
return cur.key
def floor_key(self, key):
if not key: return
last_no_big_node = self.find_last_no_big_index(key)
if last_no_big_node: return last_no_big_node.key
def ceiling_key(self, key):
if not key: return
last_no_small_node = self.find_last_no_small_index(key)
if last_no_small_node:
return last_no_small_node.key
############# Test ###############
def print_all(self, head: Node):
print("Binary Tree")
self.print_in_order(head, 0, "H", 17)
print()
def print_in_order(self, head: Node, height, to, length):
if not head: return
self.print_in_order(head.right, height + 1, "v", length)
val = str(to) + "(" + str(head.key) + "," + str(head.value) + ")" + str(to)
len_m = len(val)
len_l = (length - len_m) / 2
len_r = length - len_m - len_l
val = self.get_space(len_l) + val + self.get_space(len_r)
print(self.get_space(height * length) + val)
self.print_in_order(head.left, height + 1, "^", length)
def get_space(self, num):
return " " * int(num)
def check():
sbt = SizeBalancedTreeMap()
sbt.put("d", 4)
sbt.put("c", 3)
sbt.put("a", 1)
sbt.put("b", 2)
# sbt.put("e", 5);
sbt.put("g", 7)
sbt.put("f", 6)
sbt.put("h", 8)
sbt.put("i", 9)
sbt.put("a", 111)
print(sbt.get("a"))
sbt.put("a", 1)
print(sbt.get("a"))
for i in range(sbt.size()):
print(sbt.get_index_key(i), sbt.get_index_value(i))
sbt.print_all(sbt.root)
print(sbt.first_key())
print(sbt.last_key())
print(sbt.floor_key("g"))
print(sbt.ceiling_key("g"))
print(sbt.floor_key("e"))
print(sbt.ceiling_key("e"))
print(sbt.floor_key(""))
print(sbt.ceiling_key(""))
print(sbt.floor_key("j"))
print(sbt.ceiling_key("j"))
sbt.remove("d")
sbt.print_all(sbt.root)
sbt.remove("f")
sbt.print_all(sbt.root)
check()
